История математики, теоретический минимум
Материал из eSyr's wiki.
(→Аналитическая машина Беббиджа) |
(→Аналитическая машина Беббиджа) |
||
| Строка 303: | Строка 303: | ||
Бэббидж сформулировал принципы вычисления таблиц разностным методом при помощи машины, которую он впоследствии назвал разностной. Эта машина должна была производить комплекс вычислений, используя только операцию сложения. В 1819 году Чарльз Бэббидж приступил к созданию малой разностной машины, а в 1822 году он закончил её строительство и выступил перед Королевским Астрономическим обществом с докладом о применении машинного механизма для вычисления астрономических и математических таблиц. Он продемонстрировал работу машины на примере вычисления членов последовательности. Работа разностной машины была основана на методе конечных разностей. Малая машина была полностью механической и состояла из множества шестерёнок и рычагов. В ней использовалась десятичная система счисления. Она оперировала 18 разрядными числами с точностью до восьмого знака после запятой и обеспечивала скорость вычислений 12 членов последовательности в 1 минуту. Малая разностная машина могла считать значения многочленов 7-ой степени. | Бэббидж сформулировал принципы вычисления таблиц разностным методом при помощи машины, которую он впоследствии назвал разностной. Эта машина должна была производить комплекс вычислений, используя только операцию сложения. В 1819 году Чарльз Бэббидж приступил к созданию малой разностной машины, а в 1822 году он закончил её строительство и выступил перед Королевским Астрономическим обществом с докладом о применении машинного механизма для вычисления астрономических и математических таблиц. Он продемонстрировал работу машины на примере вычисления членов последовательности. Работа разностной машины была основана на методе конечных разностей. Малая машина была полностью механической и состояла из множества шестерёнок и рычагов. В ней использовалась десятичная система счисления. Она оперировала 18 разрядными числами с точностью до восьмого знака после запятой и обеспечивала скорость вычислений 12 членов последовательности в 1 минуту. Малая разностная машина могла считать значения многочленов 7-ой степени. | ||
| - | =Аналитическая машина | + | =Аналитическая машина Бэббиджа= |
Аналитическая машина (принцип - зубчатые передачи): (по лекциям Вали) | Аналитическая машина (принцип - зубчатые передачи): (по лекциям Вали) | ||
Версия 21:12, 9 декабря 2009
Главные достижения и основные черты математики Древнего Египта
Древний Египет. Нил --- наиболее благополучная из таких рек. Поскольку, не меняло почти русло Что они умели: арифметика, например, 10х12=24+96=120. Использовали дроби? Использовали, но только вида 1/n. Была таблица для представления дробей вида 2/n, как сумму аликвтных дробей. Были как особые 2/3 и 3/4. Как они записывали сумму дробей: 1/2 1/5 1/7 Что умели в геометрии? Считать площадь треугольника, прямоугольника, трапеции, круга. Площадь круга --- 8/9 d^2/ Умели вычислять объём цилиндра, объём усечённого конуса. Есть задачи на сумму геометрической прогрессии. Задача на пропорциональное деление. Основные результаты лектор перечислил. Математика носила прикладной, а не алгоритмический характер. Ещё одно достижение --- ритуальные сооружения, пирамиды.
Имеется два основных источника о состоянии математики в древнем Египте: Лондонский папирус, содержащий 84 задачи и Московский папирус с 25 задачами. Лондонский папирус, известный еще как папирус Ринда (по имени открывшего его ученого) был написан около 1650 г. до н.э. и хранится в Британском музее. Московский папирус написан примерно двумя столетиями раньше. Он был расшифрован в 30-е годы XX века русским академиком В.В.Струве и хранится в Музее изобразительных искусств им. А.С.Пушкина. Изложенная в папирусах математика основана на десятичной иероглифической системе. Каждая десятичная единица более высокого разряда обозначалась своим иероглифом. Нам известна римская система, основанная на том же принципе. Здесь узловые числа суть
I, V, X, L, C, D (1, 5, 10, 50, 100, 500, 1000).
Остальные числа образуются приписыванием с той или другой стороны от узлового числа других узловых чисел и повторением их.
На этой системе египтянами построена довольно сложная арифметика. Умножение здесь сводится к повторным сложениям. Замечательной чертой является действие с дробями. Все дроби сводятся к суммам основных дробей 1/n и некоторых индивидуальных, например, 2/3, 3/4. Это делается на основе таблиц разложения дробей вида 2/n (n = 3-101). Египтяне знали площадь треугольника - половина произведения основания на высоту, объем параллелепипеда, кругового цилиндра. Замечательный результат - объем усеченной пирамиды с квадратным основанием где а, b - длины сторон квадратов, h - высота. Площади круга диаметра d вычислялась как что дает для p значение 3.1605.
Главные достижения и основные черты математики Древнего Вавилона
Что прежде всего хочет сказать о Вавилоне: система счисления. Они первые использовали позиционную систему счисления с основание 60. Из этой системы счисления писались маленькие таблички. До нас дошло примерно 200 дощечек с таблицами без текста и 50 табличек с математическими текстами.
Решали задачи, сводящихся к уравнению первой, второй, третьей степени. По существу, можно говорить, что вавилоняне решали частные задачи вида ax=b, ax^2=b, x^3=a, x^2*(x+1)=a, а также системы уравнений. В Египте такого не было.
Геометрические представления вавилонян. У них есть таблица пифагоровых чисел. Теорему Пифагора в чистом виде не знали, но на таблице есть. Умели вычислять зачатки выч. углов и тригонометрических соотношений. Вычисляли площади и объёмы прямолинейных фигур. Для площади круга была формула:c^2/12, где c --- длин окружности. Отсюда π=3
Встречались следующие задачи: через какое время удвоится сумма, выданная под 20 процентов годовых.
Примерно в то же время, что и в Египте возникает второй очаг цивилизации в долине рек Тигр и Евфрат. Среднюю и южную часть равнины назвали Месопотамией (Междуречье) - это примерно современный Ирак. Южнее современного Багдада приблизительно с ХХ века до VI века до н.э. существовало рабовладельческое государство Вавилония со столицей Вавилон возле Багдада.
Математика в древнем Вавилоне была на более высоком уровне чем в Египте. Вавилоняне имели более прогрессивную позиционную 60-ричную систему счисления. Такая система имеет огромное преимущество при вычислениях по сравнению с римскими цифрами. Однако эта система не имела нуля, что приводило к некоторой неопределенности, и точное истолкование записи надо было извлекать из контекста.
Шестидесятиричная система и позиционность оказались достоянием человечества. Современное деление часа на 60 минут и 3600 секунд восходит к Вавилону. Это же относится к делению окружности на 3600 , градуса на 60 минут, минуты на 60 секунд. Что касается авторства позиционности системы, то здесь не все ясно. Возможно это изобретение Индии, где десятичная позиционная система с нулем появилась около 500 года до н.э.
В Вавилоне владели техникой решения квадратных уравнений, тогда как египтянам были известны лишь линейные. Решали также задачи, сводящиеся к кубическим и биквадратным уравнениям. Такие задачи они формулировали только для определенных числовых значений коэффициентов. Ван дер Варден в книге “Пробуждающаяся наука” указывает, что вавилоняне умели решать 10 видов уравнений и систем.
Кроме того они умели находить сумму арифметической прогрессии и суммы других видов, например,
Геометрические знания были выше египетских, уже встречаются некоторые тригонометрические соотношения. Площадь круга. Есть основания полагать, что в Вавилоне была известна теорема Пифагора.
Главные достижения и основные черты математики Древней Греции. Переход в математике от вопроса «как?» к вопросу «почему?»
постепенно сошла на нет значимость цивилизации Египта, Вавилона, и постепенно центр тяжести науки, культуры, развития цивилизации перемещался в Европу. Обычно это называется чудом Древней Греции. Что характерно для этого периода? Древние греки создали основы того, что сейчас называется элементарная математика. Что этому способствовало? Прежде всего, переход от бронзы к железу, развитие ремёсел, производства, потом появились деньги, что в значительной степени способствовало торговле, обмену. Не последнюю роль играл более удобный алфавит. Развитие алфавита --- возможность перемещения, обмена.
С чьими именами связываем первые серьёзные достижения? Документально --- Фалес Милетский 624---547 год до н.э. Он многим удивлял своих современником. Вообще говоря, это был философ. Тогда не было понятия философ или биолог или астроном, и занимались всем интересным. Считал, что главное --- вода. Предсказал затмение, Вычислял высоту пирамиды по тени. Что самое главное: он формулировал математические утверждения и их доказывал. Вот в чём принципиальное отличие математики Древней Греции --- они отвечали не только на вопрос как, но и почему. Какие факты формализовывал и доказывал он: Диаметр делит круг пополам Вертикальные углы равны В равнобедренном треугольнике углы равны В ... равны по двум углам Теорема Фалеса
Вот какие важные факты сформулировал и доказал он в 6 в. до н.э.
Например, Фалес умел вычислить расстояние до корабля от берега.
Что ещё хотелось бы сказать пр математику этого периода ... хотел построить тоннель через гору Кастор. Что надо было сделть: в определённом месте начать рыть тоннель и в определённом месте выйти.
Он построил матмодель...
Далее --- школа Пифагора Самосского.
Это то, что уже считается классикой.
Прежде всего, Пифагор искал основу всего сущего, и он считал таковой основой число. Не только чётные и нечётные, но и совершенные, дружественные (сумма делителей одного равна другому и наоборот, напр. 220 и 284). Пифагор обожествлял эти понятия и представления. И он считал, что с числами могут общаться только избранные. Какие ещё были числа: треугольные, квадратные. У него возникло понятие иррацинальности, когда пытался найти общую меру у стороны квадрата и диагонали. Тогда же было доказано, что корень из двух есть число иррациональное. Это первый кризис в истории математики. Что-то нельзя представить в виде числа, нельзя найти общую меру двух отрезков, обнаружилось, что множество отрезков более мощное, чем множество чисел. Поэтому дальше были геометрические задачи.
. К VII веку дол н.э. Греция состояла из совокупности государств - полисов (городов), ведущих оживленную торговлю между собой и соседними государствами: Египтом, Персией (современный Иран), Финикией (государство, расположенное на восточном побережье Средиземного моря) и др. В это время в Греции высокого уровня достигли культура, техника, наука. До нашего времени дошли прекрасные памятники архитектуры и скульптуры. Большое развитие получила философия, астрономия, математика. Надежных источников, описывающих ранний период развития греческой математики нет. Однако наука располагает изданиями великих античных математиков Евклида, Архимеда, Аполлония, живших позднее ( IV - II в. до н.э.).
Характерной чертой греческой математики в отличие от Египта и стран Востока является стремление доказывать математические факты. Родоначальником греческой математики считается Фалес (625 - 547 г. до н.э.). Ему приписывают доказательства ряда математических результатов : диаметр делит круг пополам, углы при основании равнобедренного треугольника равны и многое другое. Греки сумели в течение одного - двух столетий овладеть математическим наследием предшественников, которое накапливалось тысячелетиями, и по-новому его осмыслить.
В математике этого периода практические задачи, связанные с вычислениями, геометрическими измерениями и построениями, продолжали играть большую роль. Эти задачи постепенно выделились в отдельную область математики, названную логистикой. Она включала операции с целыми числами и дробями, решение задач, сводящихся к уравнениям 1-й и 2-й степени, практические задачи архитектуры, земледелия и т.п.
В то же время уже в школе Пифагора (580 - 500 г. до н.э.) начинается процесс накопления и систематизации абстрактных математических фактов. Пифагорийцы не признавали прикладного характера математики. Будучи аристократами они считали, что решение практических задач - удел лишь низших сословий.
Пифагорийцами была построена значительная часть планиметрии прямолинейных фигур, доказана теорема Пифагора ( она получила имя основателя греческой школы, хотя была известна значительно раньше в Вавилоне). Был найден способ отыскания целых пифагоровых чисел, удовлетворяющих соотношению : для нечетных n они имеют вид
.
Для четных n пифагоровы числа были получены позже в Академии знаменитого греческого философа Платона (427 - 347 г до н.э.) и равны
Из арифметики была выделена в отдельную область теория чисел - все, что относится к общим свойствам операций с натуральными числами. Целые числа представлялись основополагающими универсальными объектами, к операциям с которыми должны сводится и все математические построения, и вообще все многообразие явлений действительности. “Все есть число и все из чисел” - руководящий принцип пифагорийцев. Из этого принципа следовало, что отношения между любыми количествами должны быть отношениями целых чисел (т.е. рациональными числами в современной терминологии). Этому обожествлению целых чисел был нанесен сокрушительный удар самими же пифагорийцами. Оказалось, что отношение диагонали квадрата к его стороне ( равное ) не является рациональным числом, т.е. отношением целых чисел. Этот факт был доказан путем сведения к противоречию. Действительно, пусть где p и q - взаимно простые. Тогда и p - четное, а, значит, q - нечетное. Но из того, что следует , т.е. , а следовательно и q четные. Это был, по сути, первый кризис в математике. В то время еще не было предпосылок разрешить его, расширив понятие числа вводом иррациональностей. Осознав, что совокупность геометрических величин более полна, чем множество рациональных чисел, греки создали исчисление в геометрической форме. Новое исчисление получило в литературе название геометрической алгебры. В греческой математике возникла еще одна трудность, связанная с понятием бесконечности. Математики понимали, что за целым числом N следует целое число N+1, затем N+2 и так далее до бесконечности. К бесконечным процессам приводил и метод исчерпывания (предела), о котором речь будет идти ниже. Эта концепция была важным достижением, однако противоречила всем имеющимся тогда данным физики и философским воззрениям о конечности Вселенной. Она открывала новые широкие возможности в математике, но приводила к парадоксам. Смысл понятия бесконечности и до сих пор не раскрыт до конца, однако в течение веков на многие вопросы, возникающие в связи с этим понятием получен ответ. Еще одна трудность связана с тем, что греки не знали отрицательных чисел. Они имели дело с отрицательными числами только в терминах алгебраических выражений для площадей квадратов и прямоугольников, например, . Отрицательные числа впервые использовались, по видимому, китайцами, однако окончательно вошли в математику после работ Кардано в 1545 году.
Демокрит – считал, что все тела состоят из атомов. 1-м рассмотрел стереометрию. Метод исчерпывания-чтобы измерить площадь фигуры, надо последовательно вписывать аппроксимирующие фигуры (существование – через построение, единственность не рассматривалась)
Платон(437-347 до нэ)-геометрия, стереометрия, идея предельного перехода.
Аристотель(384-322 до нэ)-любое движение может быть получено по окружности и прямой. Достижения в логике(аналогия, дедукция, инфукция)
Архимед(287-212 до нэ)- "Эврика!" (закон Архимеда), оборона Сиракуз: воины, вставшие параболой и поджегшие корабль, всякие военные машины и чертежи на песке. Достижения - линии, круг, площади методами в духе интегралов, оценки значения пи через периметры правильных многоугольников, теорема о промежуточных значениях непрерывной функции, площади и объемы фигур через суммы Дарбу - главный результат (на своей могиле Архимед завещал выбить шар, вписанный в цилиндр). Трактат о количестве песчинок во Вселенной.
Два достижения греческой математики далеко пережили своих творцов.
• греки построили математику как целостную науку с собственной методологией, основанной на чётко сформулированных законах логики (гарантирующих истинность выводов при условии, что истинны предпосылки).
• они провозгласили, что законы природы постижимы для человеческого разума, и математические модели — ключ к их познанию.
«Начала» Евклида
(300 до нэ) 13 книг Начал (или элементов) Евклида, в которых приведена вся современная математика в систему.
В первых четырех книгах рассматривается геометрия на плоскости. В 5-ой и 6-ой книгах изложена теория отношений Евдокса и применена к подобию треугольников. Книги 7-9 посвящены теории чисел (теория делимости, алгоритм Евклида, теория простых чисел). В 10-й книге дана геометрическая классификация квадратичных и биквадратичных иррациональностей, т.е. чисел вида 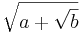 . В последних трех книгах излагается геометрия в пространстве. Изложение завершается изучением правильных многогранников: тетраэдра(4 грани), куба (6), октаэдра (8), додэкаэдра (12) и икосаэдра (20). Доказывается, что их только пять. Они получили название платоновых тел и имели основополагаюшее значенние в космологии школы Платона.
. В последних трех книгах излагается геометрия в пространстве. Изложение завершается изучением правильных многогранников: тетраэдра(4 грани), куба (6), октаэдра (8), додэкаэдра (12) и икосаэдра (20). Доказывается, что их только пять. Они получили название платоновых тел и имели основополагаюшее значенние в космологии школы Платона.
Таким образом, в “Началах” систематизированы и строго изложены результаты, полученные математикой к III веку до н.э., включающие три важнейших открытия математики древности: теорию отношений Евдокса, теорию иррациональных Теэтета и теорию пяти правильных тел.
Одним из первых крупных ученых, связанных с Александрией, был Евклид, живший около 300 г. Ничего, кроме научных трудов, о его биографии не известно. Евклид - один из наиболее влиятельных математиков всех времен. Наиболее знаменитое его произведение “Начала”. Это первое значительное произведение, дошедшее до нас полностью. В истории Западного мира это, повидимому, второе после Библии произведение по числу изданий. После изобретения книгопечатания (в Европе в XV веке) оно издавалось более 1000 раз. Большая часть школьной геометрии заимствована из “Начал”. Логическое построение “Начал” повлияло на научное мышление больше, чем какое-либо иное произведение. Оно основывается на строго логическом выводе теорем из системы определений, постулатов и аксиом.
“Начала” состоят из 13 книг. В первых четырех книгах рассматривается геометрия на плоскости. В 5-ой и 6-ой книгах изложена теория отношений Евдокса и применена к подобию треугольников. Книги 7-9 посвящены теории чисел (теория делимости, алгоритм Евклида, теория простых чисел). В 10-й книге дана геометрическая классификация квадратичных и биквадратичных иррациональностей, т.е. чисел вида . В последних трех книгах излагается геометрия в пространстве. Изложение завершается изучением правильных многогранников: тетраэдра(4 грани), куба (6), октаэдра (8), додэкаэдра (12) и икосаэдра (20). Доказывается, что их только пять. Они получили название платоновых тел и имели основополагаюшее значенние в космологии школы Платона.
Таким образом, в “Началах” систематизированы и строго изложены результаты, полученные математикой к III веку до н.э., включающие три важнейших открытия математики древности: теорию отношений Евдокса, теорию иррациональных Теэтета и терию пяти правильных тел.
Остановимся специально на аксиоматике “Начал”. Греки уже владели несколькими явными и несомненными истинами окружающего мира, такими как :две точки определяют прямую, прямую можно продолжить неограниченно в обе стороны, прямые углы равны, если к равным прибавить равные, получим снова равные. Эти аксиомы вошли в число аксиом и постулатов “Начал”, из которых Евклид вывел около 500 теорем. Особое место занимает аксиома о параллельных, согласно которой через точку вне заданной прямой можно провести одну и только одну прямую, параллельную ей. Эта аксиома не поддается проверке опытом. Многие ученые делали попытку доказать ее как теорему, исходя из остальных девяти аксиом Евклида, но безуспешно. Лишь в XIX веке это утверждение было окончательно признано аксиомой.
Математика Ближнего Востока (IX-XVв.)
Аль-Хорезми: возникновение рецептов в виде алгоритмов. Алгебраический трактат. Решение различных квадратных уравнений с положительными коэффициентами (достигается перебрасыванием в соответствующую часть для смены знака). Написал трактат об индийских числах, работал в десятичной и шестидесятеричной системах счисления.
Омар Хайям (1043--1123): поэт-математик. "Алгебра - наука об уравнениях". Пытался искать решения уравнений третьей степени в виде общих точек конических сечений. Делал попытки доказать пятый постулат Евклида.
Насиред-дин: построил первую систему плоской и сферической тригонометрии. Тоже пытался доказать пятый постулат.
Улугбек (1394--1449), правитель Самарканда. Много внимания уделял науке. Построил в Самарканде обсерваторию и медресе (университет). Составил таблицу синусов (точнее, хорд) с точностью до девятого знака и с шагом в одну минуту.
Аль-Каши (XIII в.). Итерационные решения уравнений 2 степени. Вычислил 17 знаков \pi, построив правильный 3*2^28-угольник.
Индия
Индийская нумерация изначально была изысканной. В санскрите были средства для именования чисел до 1050. Для цифр сначала использовалась сиро-финикийская система, а с VI века до н. э. — написание «брахми», с отдельными знаками для цифр 1-9. Несколько видоизменившись, эти значки стали современными цифрами, которые мы называем арабскими, а сами арабы — индийскими.
Около 500 г. н. э. неизвестный нам великий индийский математик изобрёл новую систему записи чисел — десятичную позиционную систему. В ней выполнение арифметических действий оказалось неизмеримо проще, чем в старых, с неуклюжими буквенными кодами, как у греков, или шестидесятиричных, как у вавилонян. В дальнейшем индийцы использовали счётные доски, приспособленные к позиционной записи. Они разработали полные алгоритмы всех арифметических операций, включая извлечение квадратных и кубических корней.
К V—VI векам относятся труды Ариабхаты, выдающегося индийского математика и астронома. В его труде «Ариабхатиам» встречается множество решений вычислительных задач. В VII веке работал другой известный индийский математик и астроном, Брахмагупта. В нём изложены учение об арифметической прогрессии (известное правило её суммирования) и решение квадратных уравнений, имеющих действительное решение
Наибольшего успеха средневековые индийские математики добились в области теории чисел и численных методов. Использовали отрицательные числа( как долг). Комбинаторика. Суммирование рядов. Тригонометрия. В алгебре - еще один шаг к обобщению уравнений.
Арабы
Математика Востока, в отличие от греческой, всегда носила более практичный характер. Соответственно наибольшее значение имели вычислительные и измерительные аспекты. Основными областями применения математики были торговля, ремесло, строительство, география, астрономия и астрология, механика, оптика.
Аль-Хорезми: возникновение рецептов в виде алгоритмов. Алгебраический трактат. Решение различных квадратных уравнений с положительными коэффициентами (достигается перебрасыванием в соответствующую часть для смены знака). Написал трактат об индийских числах, работал в десятичной и шестидесятеричной системах счисления.
Омар Хайям (1043--1123): поэт-математик. "Алгебра - наука об уравнениях". Пытался искать решения уравнений третьей степени в виде общих точек конических сечений. Делал попытки доказать пятый постулат Евклида.
Насиред-дин: построил первую систему плоской и сферической тригонометрии. Тоже пытался доказать пятый постулат.
Улугбек (1394--1449), правитель Самарканда. Много внимания уделял науке. Построил в Самарканде обсерваторию и медресе (университет). Составил таблицу синусов (точнее, хорд) с точностью до девятого знака и с шагом в одну минуту.
Аль-Каши (XIII в.). Итерационные решения уравнений 2 степени. В «Трактате об окружности» ал-Каши вычисляет длину окружности по рецепту Архимеда — как среднее арифметическое между периметрами вписанного и описанного правильных многоугольников с числом сторон . Это дало ему приближение π = 3,14159265358979325, где неверна только последняя цифра 5, которую следовало бы заменить на 4.
Первые инструменты для счёта - абаки
Абак — счётная доска, применявшаяся для арифметических вычислений приблизительно с IV века до н. э. в Древней Греции, Древнем Риме.
Реконструкция римского абака
Доска абака была разделена линиями на полосы, счёт осуществлялся с помощью размещённых на полосах камней или других подобных предметов.
Впервые появился, вероятно, в Древнем Вавилоне ок. 3 тыс. до н. э. Первоначально представлял собой доску, разграфлённую на полосы или со сделанными углублениями. Счётные марки (камешки, косточки) передвигались по линиям или углублениям. В 5 в. до н. э. в Египте вместо линий и углублений стали использовать палочки и проволоку с нанизанными камешками.
В Европе абак применялся до XVIII века. В Средние века сторонники производства арифметических вычислений исключительно при помощи абака — абацисты — в течение нескольких столетий вели ожесточённую борьбу с алгоритмиками — приверженцами возникших тогда методов алгоритмизации арифметических действий.
В России счёты (аналог абака) появились в XVI веке и применяются до сих пор, хотя в последнее время их использование ограничено широким распространением калькуляторов.
Ацтекские счёты возникли приблизительно в X веке и изготавливались из зёрен кукурузы, нанизанных на струны, установленные в деревянной раме.
В странах Востока распространены китайский аналог абака — суаньпань и японский — соробан.
Логарифмы, логарифмическая шкала, логарифмические линейки. Непер, Гюнтер, Отред, Деламейн, Уатт, Ньютон
Николас Меркатор (1620-1681). Умел вычислять логарифм от 1+х через разложение в ряд:
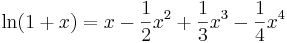
Логарифмические линейки: впервые изобрел Отред в 1620-23, затем совершенствовали Ньютон, Уатт. Вроде бы в 1654 Р. Бесакер изобрел криволинейную логарифмическую линейку.
Техника, математика... сплетались в причудливом танце времени.
Джон Непер (1550--1617) В 1614 опубликовал работу "Замечательные таблицы логарифмов" - логарифмы и тригонометрические функции(0-90 градусы,шаг 1 минута) с точностью до восьмого знака.
1617 - проф. Бриг из Лондона, 8-значные таблицы чисел от 1 до 1000. Затем он же логарифмы - от 1 до 20000, 80000-100000.
Эдвард Гюнтер: логарифмическая шкала. На дощечке наносил логарифмы чисел, затем измерительным циркулем мерял расстояния - разности и суммы.
Открытия математики эпохи Возрождения. Кардано, Тарталья, Сципион дель Ферро и др
Ферро. Думал над решением уравнения третьей степени. х^3 + ax = b. (Glider: википедия говорит, что он даже научился их решать)
Это не то же самое, чем если бы было с переносом слагаемых в другую часть - отрицательных чисел не было. Общих формул тоже не было (для произвольных коэффициентов). У него получилось)
Был ещё человек Никколо Тарталья (итальянец). Когда французы входили в Болонию, то осколком разрыва его ранило в гортань, и он стал заикаться. Тарталья в переводе и есть заика. =) Он был сыном довольно бедного человека, что даже в школе учился только очень недолго и в самых начальных классов. И деньги кончились очень быстро. И тем не менее он продолжал самообразование, и стал в результате довольно известным человеком во многих сферах. В частности, Тарталья изучал уравнения третьей степени. Артиллеристы спросили: под каким углом надо стрелять, чтобы дальше всего улетел снаряд? Он сказал - 45 градусов. Правда, есть сомнения, что он мог это доказать - скорее всего, чисто эмпирически. Также он интересовался математическими проблемами, в частности, решением уравнения, что было написано чуть раньше. И в Италии был соревновательный дух. И было так: два человека вызывали друг друга на дуэль (математическую), в присутствии кучи людей. И каждый выдавал друг другу задачи, и кто больше задач решил. И если решить на n задач меньше, то n человек из группы поддержки могли обедать у противоположной стороны.) Фиоре вызвал Тарталью на дуэль, дал 30 задач того же типа (все!). В общем, он их все решил.) И победил. Фиоре не решил одну из задач. =) Но плагиата раньше не существовало. А тут уже наступили авторские права: важен вопрос, кто конкретно это сделал. Поэтому каждый держал свои рецепты в секрете, в т.ч. и Тарталья.
Кардано родился в том же году, что и Тарталья. Он был незаконнорожденный сын адвоката, получил хорошее медицинское образование, но не был принят в коллегию врачей (ибо незаконнорожденный). Кроме медицины, очень любил азартные игры. В частности, игру в кости.) В результате заложил основы теории вероятностей, грубо сформулировал закон больших чисел. Ввел понятие "софистических" (мнимых) чисел В 39 году послал к Тарталье с просьбой раскрыть рецепт решения уравнения третьей степени. Долго уговаривал, поймал на тщеславии. Встретились, при встрече был Фиоре.. В общем, выпросил рецепт. Опубликовал в 41 году одну из работ, не упомянув, откуда у него эти записи. В 45 году издал свою большую книжку, => клятвопреступник (поклялся не печатать и никому не говорить то, что дал ему Тарталья) (Glider: википедия говорит, что Кардано прочел неопубликованную работу дель Ферро, поэтому счел себя вправе нарушить обещание). Всё это формулировалось и доказывалось на языке геометрии. Алгебраической символики не было. Поэтому нельзя было подставить и проверить, что это так и есть).
Зарождение математики переменных величин. Декарт, Ферма, Кепплер, Кавальери, Паскаль и др
Рене Декарт (1595-1650) Сущность есть трёхмерность материи 1637 - публикация труда "Геометрия". Сформулировал понятие переменной величины и сказал о поняти прямоугольной системе координат. Переменная величина - в 2х видах. Доказал, что все задачи, которые решаются с помощью циркуля и линейки, сводятся к решению уравнений не выше второй степени. Классификация кривых. Кривые имеют не степени, а ранги, а ранг кривой равен количеству звеньев шарнирного механизма, требуемых для создания такого рисунка, а те, кого так не нарисуешь - назвал механическими (а потом их назвали трансцендентными). Не любил отрицательные числа и ничего не знал о мнимых числах. Но высказал гипотезу, что уравнение n-ной степени имеет n корней. Однако ограничивался алгебраическими кривыми. Но зато начал использовать удобные обозначения.
Пьер Ферма (1601-1665) Современник Декарта. Образование юридическое. Тоже неотрицательные числа; применял некоторые преобразования (сдвиг и поворот) - это то, тчо его отличало от Декарта.. и это позволяло приводить уравнения к каноническому виду. Начал придумывать свои способы вычисления площадей и объёмов. Придумал книжку. Там написал свои методы интегрирования, перекликающиеся с методами Евдокса и Архимеда. 92 вида фигур вращения.
Иоганн Кеплер Ну про него мы и так всё знаем...
Кавалерия Ученик Галилея. Монах. Увлекался математикой (странно...). Необразованный монах, поэтому изобретал велосипед, причём не один раз. И теория у него была - теория неделимых. Есть материя в пространстве - пусть камень. Короче, заключал n-мерное тело в m k-мерных, где k<n. Опть считал объёмы.
Блез Паскаль (1623--1662) Родился в достаточно обеспеченной семье рантье Этьена Паскаля. В 1638 отец попал в немилость к Ришелье и вынужден был бежать в Испанию. Позже по просьбе младшей дочери Этьен был прощен и занял пост интенданта Руана. В шестнадцатилетнем возрасте Блез опубликовал первую работу по математике (на 53 строки математического труда, размножил в 50 экземплярах и расклеил по улицам Парижа). Это был трактат по проективной геометрии "Опыт о конических сечениях"
Занимался также физикой; разработал в это же время что-то из гидродинамики (закон Паскаля). Гидравлический пресс и всё такое. Из математики: треугольник Паскаля; первые методы интегрирования; использовал начала теории определённого и неопределнного интегрирования. Определённые результаты теории вероятности. В общем, везде он начал что-то делать.
В 18 лет начал разрабатывать вычислительные машины (около 50 штук). Идеи очень напоминали Шиккардовские. Но он точно не мог их увидеть, потому что никто о той машине и её идеях, кроме самого Шиккарда и его друзей, не знал этих идей. Машина Паскаля умела складывать, вычитать (используя дополнительный код), умножать и делить (путем последовательных сложений или вычитаний)
Счётные машины эпохи техники часовых механизмов (Шиккард, Паскаль, Лейбниц)
1957г.: Хаммер обнаружил в Штутгарте наброски вычилительной машины, созданной Шиккардом в 1623 году. Так что примерно раньше, чеми Паскаль придумал свою машину, он нашёл запись, где это было придумано. Но это обнаружилась копия. А оригинал был в России в библиотеке Пулковской обсерватории (архив Кеплера). Ещё через 10 лет в библиотеке Мадрида обнаружилось устройство суммирования Леонардо да Винчи. Примитивно. Но умела. Сделал Ферма, она вроде как даже работала.
Шиккард (1592--1636) Профессор кафедры восточных языков Тюбингенского университета, интересовался астрономией, переписывался с Кеплером. Кеплер высоко ценил его способности. Рекомендовал бросить языки и заняться математикой... что он и сделал. Стал потом заведовать кафедрой математики. В письме писал, что он сумел сделать "Часы для счёта". То есть он сделал механически то, что Кеплер сделал алгебраически. Придумал устройство, которое умело складывать, вычитать, умножать и делить. Умножать и делить, смысл: чем отличается машина Шиккарда от абака и от всех более ранних вообще? Проблемы: как представлялось число; не как колечко, а цифра - угол поворота зубчатого колеса. 10 зубцов. Самая тяжёлая задача - перенос десятков. Поставили ещё одно однозубое колесо. =) В общем, она отличалась тем, что была сделана остроумно.)
В машине также использовались барабаны, на которые была намотана таблица умножения. Блез Паскаль (1623--1662) Родился в достаточно обеспеченной семье рантье Этьена Паскаля. В 1638 отец попал в немилость к Ришелье и вынужден был бежать в Испанию. Позже по просьбе младшей дочери Этьен был прощен и занял пост интенданта Руана. В шестнадцатилетнем возрасте Блез опубликовал первую работу по математике (на 53 строки математического труда, размножил в 50 экземплярах и расклеил по улицам Парижа). Это был трактат по проективной геометрии "Опыт о конических сечениях"
Занимался также физикой; разработал в это же время что-то из гидродинамики (закон Паскаля). Гидравлический пресс и всё такое. Из математики: треугольник Паскаля; первые методы интегрирования; использовал начала теории определённого и неопределнного интегрирования. Определённые результаты теории вероятности. В общем, везде он начал что-то делать.
В 18 лет начал разрабатывать вычислительные машины (около 50 штук). Идеи очень напоминали Шиккардовские. Но он точно не мог их увидеть, потому что никто о той машине и её идеях, кроме самого Шиккарда и его друзей, не знал этих идей. Машина Паскаля умела складывать, вычитать (используя дополнительный код), умножать и делить (путем последовательных сложений или вычитаний)
Готфрид Вильгельм Лейбниц (1646-1716) Родился в Лейпциге в семье профессора этики, морали и права. Имел очень хорошие отношения с Петром I. Одна из его деятельностей - дипломатия на высоком уровне; занимался монетным делом, как и все умные люди; насоветовал всего хорошего Петру. В частности, по его совету была придумана Питерская Академия Наук. В общем, он везде приложил руку, даже в церкви. В первую очередь искал "всеобщую характеристику" - общий метод познания всех истин вообще. В ее основе, по мнению Лейбница, лежала математика. Если мы формализуем все знания, то споры философов станут не нужны - формализуем всё, и всё.) В результате был сделан значительный вклад в математическую логику. Член Лондонского Королевского общества, и много чего ещё, признание он получил. Хотя, он был и не настолько замечателен, как, например, Ньютон. В конце жизни поимел разлад с окружающим миром... почему - хз. Ввёл дифференциал (dx, ага). Вообще сделал много в дифференциальном исчислении. Знак интеграла ввёл, константа, переменная, координаты, абсцисса, дифференциальное уравнение, функция, алгебраические трансцендентные кривые. В области дифференцирования: правила дифференцирования суммы, разности, степени, корня, произведения, и т.д. Формула многократного дифференцирования произведения функций, разлагал функции в степенные ряды для оперирования со сложными функциями; установил сходимость знакочередующегося ряда; вычислил пи как разложение в ряд. Правило Крамера придумал Лейбниц.) Правило Лопиталя впервые появилось тоже в его трудах. Правда, его изначально придумал Бернулли... Придумал определитель, кстати. Машина Лейбница, да. Когда ему было 24 года, он задумал усовершенствовать машину Паскаля. Ему в ней не нравилось умножение как последовательное сложение, там нужно было устанавливать всё время второе слагаемое. В машине Лейбница это было автоматизировано, интересная реализация: использовался ступенчатый валик; сходный принцип применялся в XIX-XX вв. в арифмометрах. Начал в 1676 году, несколько раз усовершенствовал, закончил в 1694 году. Машины были очень дорогими, сложными, техники тяжеловато с этим справлялись. Зато сам не вытачивал детали, как Паскаль.
Научная биография Ньютона. Теория флюксий
Исаак Ньютон (1642-1727) Учился в Triniti-колледже =) закончил бакалавром (в 1665). Спрятался от чумы в своём имении и жил там 3 года, никого не любя и никем не любимый. Поэтому учился. Натворил.... как Пушкин. Заложил основы интегрального и дифференциального исчисления. Придумал зеркальный телескоп и от нечего делать его сам сделал. Открыл закон всемирного тяготения. Занимался опытами по дифракции, интерференции, раскладывал спектр света. Сильно воевал с Гуком, ибо был приверженцем корпускулярной теории света, а Гук - волновой. Но длину световой волны замерил Ньютон =) И был принят в Лондонское Королевское Общество. В 1703 году его возглавил.
1671 - "Метод флюксий и бесконечные ряды" Математический аппарат у него - не цель, а средство. Книга "Мат. начала натурфилософии". Издал её в 1688 году. И всё там считал через свою математику. Кстати, он её нигде не афишировал.
Флюксией Ньютон называл производную, а флюэнтой - первообразную.
Научная биография Лейбница. Дифференциальное исчисление
Готфрид Вильгельм Лейбниц (1646-1716) Родился в Лейпциге в семье профессора этики, морали и права. Имел очень хорошие отношения с Петром I. Одна из его деятельностей - дипломатия на высоком уровне; занимался монетным делом, как и все умные люди; насоветовал всего хорошего Петру. В частности, по его совету была придумана Питерская Академия Наук. В общем, он везде приложил руку, даже в церкви. В первую очередь искал "всеобщую характеристику" - общий метод познания всех истин вообще. В ее основе, по мнению Лейбница, лежала математика. Если мы формализуем все знания, то споры философов станут не нужны - формализуем всё, и всё.) В результате был сделан значительный вклад в математическую логику. Член Лондонского Королевского общества, и много чего ещё, признание он получил. Хотя, он был и не настолько замечателен, как, например, Ньютон. В конце жизни поимел разлад с окружающим миром... почему - хз. Ввёл дифференциал (dx, ага). Вообще сделал много в дифференциальном исчислении. Знак интеграла ввёл, константа, переменная, координаты, абсцисса, дифференциальное уравнение, функция, алгебраические трансцендентные кривые. В области дифференцирования: правила дифференцирования суммы, разности, степени, корня, произведения, и т.д. Формула многократного дифференцирования произведения функций, разлагал функции в степенные ряды для оперирования со сложными функциями; установил сходимость знакочередующегося ряда; вычислил пи как разложение в ряд. Правило Крамера придумал Лейбниц.) Правило Лопиталя впервые появилось тоже в его трудах. Правда, его изначально придумал Бернулли... Придумал определитель, кстати. Машина Лейбница, да. Когда ему было 24 года, он задумал усовершенствовать машину Паскаля. Ему в ней не нравилось умножение как последовательное сложение, там нужно было устанавливать всё время второе слагаемое. В машине Лейбница это было автоматизировано, интересная реализация: использовался ступенчатый валик; сходный принцип применялся в XIX-XX вв. в арифмометрах. Начал в 1676 году, несколько раз усовершенствовал, закончил в 1694 году. Машины были очень дорогими, сложными, техники тяжеловато с этим справлялись. Зато сам не вытачивал детали, как Паскаль.
Наука в России в начале 18-го века. Леонард Эйлер. Научная биография
При Петре стали организовываться школы, но народ не хотел учиться. В результате из-за переписки Петра с Вольфом в Россию стали приезжать сильные математики, и в том числе Эйлер и сыновья Бернулли.
Леонард Эйлер (1707-1783) Родился в Базеле, в семье священника. В 16 лет стал магистром. Занимался математикой, теологией, медициной, проблемы коралестроения, отправлял свои работы в Париж, чтобы его взяли там на кафедру, о его почему-то не взяли. Занимался морским делом во всех его проявлениях; а потом оказалось, что он безработный. В 1727 приехал в Россию и угодил в тот день, когда умерла Екатерина Первая. И это очень негативно сказалось на науке. Освободилась кафедра физики, потому что учёные сбегали из России, а потом и кафедра математики, и Эйлер их обе на себя взял.) Стал публиковаться, там же была статья Бернулли о колебаниях струны. От перенарпяжения потерял зрение на один глаз, потом уехал в Германию на некоторое время, но всё ещё помогает России всем, чем может, и в результате опять вернулся в Россию. Продолжает очень напряжённо работать и теряет зрение на второй глаз. И он диктовал свои работы (400 работ продиктовал в своём почтенном возрасте) ученикам и своему сыну.. Лаплас: "Читайте Эйлера, учителя всех нас" (с). За свою жизнь опубликовал 889 работ. Это много, ибо он это всё сам придумывал. +3000 писем математического содержания. Математика, механиеака, астрономия, медицина, морское дело, баллистика, артиллерия, финансовое дело, музыка, горное дело, теория музыки, картография, страховое дело, то есть, понимаете, всё. До хрена методов Эйлера, формул, терминов Эйлера.
Условие Коши-Римана - это Эйлер и Даламбер)) Ряды Фурье - это Эйлер =)
В 1970 (???) году - ввёл понятие двойного интеграла.
Альфа-бета-гамма функции тоже.
Самый базовый его труд - дифференциальное исчисление. Создал теорию ОДУ, основы ДУЧП. Диффур с постоянными коэффициентами... чаще всего решаются через подстановки Эйлера. Он пишет книгу и включает в неё все известные способы решения диффуров, в т.ч. и им самим изобретёнными. О единственности он не задумывался. Не разделял уже действительные и комплексные аргументы - в общем случае делал. Начал классифицировать кривые по степени.
Умер Эйлер - на долгое время математика в России заглохла.
Научная биография Ч. Беббиджа. Разностная машина Беббиджа
Чарльз Бэббидж считается изобретателем вычислительных машин. Кроме того, Бэббидж занимался безопасностью железнодорожного движения, для чего оборудовал вагон-лабораторию всевозможными датчиками, показания которых фиксировались самописцами. Изобрёл спидометр. Участвовал в изобретении тахометра. Создал приспособление, сбрасывающее случайные предметы с путей перед локомотивом. В ходе работ над созданием вычислительных машин, сделал большой прогресс в металлообработке. Сконструировал поперечно-строгальный и токарно-револьверный станки, придумал методы изготовления зубчатых колес. Предложил новый метод заточки инструментов и литья под давлением. Он содействовал реформированию почтовой системы в Англии. Составил первые надёжные страховые таблицы. Занимался теорией функционального анализа, экспериментальными исследованиями электромагнетизма, вопросами шифрования, оптикой, геологией, религиозно-философскими вопросами. В 1834 году Бэббидж написал одну из самых важных работ «Экономика технологий и производств», в которой он предлагал то, что сейчас называется «Исследованием операций».
Бэббидж сформулировал принципы вычисления таблиц разностным методом при помощи машины, которую он впоследствии назвал разностной. Эта машина должна была производить комплекс вычислений, используя только операцию сложения. В 1819 году Чарльз Бэббидж приступил к созданию малой разностной машины, а в 1822 году он закончил её строительство и выступил перед Королевским Астрономическим обществом с докладом о применении машинного механизма для вычисления астрономических и математических таблиц. Он продемонстрировал работу машины на примере вычисления членов последовательности. Работа разностной машины была основана на методе конечных разностей. Малая машина была полностью механической и состояла из множества шестерёнок и рычагов. В ней использовалась десятичная система счисления. Она оперировала 18 разрядными числами с точностью до восьмого знака после запятой и обеспечивала скорость вычислений 12 членов последовательности в 1 минуту. Малая разностная машина могла считать значения многочленов 7-ой степени.
Аналитическая машина Бэббиджа
Аналитическая машина (принцип - зубчатые передачи): (по лекциям Вали)
- Склад (память) - Мельница (АЛУ) - УУ (управление) - IO (ввод-вывод)
50 разрядов
Ввод-вывод осуществляется перфокартами (которые придумали ткачи): - принимающие - поставляющие - с сохранением информации - с за(т/п?)иранием того, откуда передаем
Были также перфокарты с программами (записью, какие действия следует выполнить) Для реализации if-then-else использовали знак результата. Но потребовалось еще передвигать перфокарты вперед и назад для реализации переходов.
Архитектура современного компьютера во многом схожа с архитектурой аналитической машины. В аналитической машине Бэббидж предусмотрел следующие части: склад (store), фабрика или мельница (mill), управляющий элемент (control) и устройства ввода/вывода информации. Склад предназначался для хранения как значений переменных, с которыми производятся операции, так и результатов операций. В современной терминологии это называется памятью. Мельница (арифметико-логическое устройство, часть современного процессора) должна была производить операции над переменными, а также хранить в регистрах значение переменных, с которыми в данный момент осуществляет операцию. Третье устройство, которому Бэббидж не дал названия, осуществляло управление последовательностью операций, помещение переменных в склад и извлечение их из склада, а также выводом результатов. Оно считывало последовательность операций и переменные с перфокарт. Перфокарты были двух видов: операционные карты и карты переменных. Из операционных карт можно было составить библиотеку функций. Кроме того, по замыслу Бэббиджа, Аналитическая машина должна была содержать устройство печати и устройство вывода результатов на перфокарты для последующего использования. Для создания компьютера в современном понимании оставалось лишь придумать схему с хранимой программой, что было сделано 100 лет спустя Эккертом, Мочли и Фон Нейманом.
Научная биография А. Лавлайс
1815-1852. Дочь лорда Байрона. Присутствовала на презентации разностной машины Беббиджа. Перевела на английский статью о аналитической машине Беббиджа. Снабдила ее комментариями относительно алгоритма и программы вычислений.В числе прочего она сообщила Бэббиджу, что составила план операций для аналитической машины, с помощью которых можно решить уравнение Бернулли, которое выражает закон сохранения энергии движущейся жидкости. подпрограмма и библиотека подпрограмм, модификация команд и индексный регистр, которые стали употребляться только в 50-х годах XX века. Сам термин «библиотека» был введён Бэббиджем, а термины «рабочая ячейка» и «цикл» предложила Ада Лавлейс. Считала, что машина может вычислить многое, если ей задать способ вычисления.
Н.И. Лобачевский и неевклидова геометрия
1792-1856. Учился и работал в Казанской университете. Он исходил из попытки доказать 5 постулат евклида. Геометрия Лобачевского (гиперболическая геометрия) — одна из неевклидовых геометрий, геометрическая теория, основанная на тех же основных посылках, что и обычная евклидова геометрия, за исключением аксиомы о параллельных, которая заменяется на аксиому о параллельных Лобачевского. Постулат Лобачевского: через точку, не лежащую на данной прямой, проходят по крайней мере две прямые, лежащие с данной прямой в одной плоскости и не пересекающие её. Лобачевский считает аксиому параллельности Евклида произвольным ограничением. С его точки зрения, это требование слишком жёсткое, ограничивающее возможности теории, описывающей свойства пространства. Евклидова геометрия может быть из нее получена предельным переходом (при стремлении кривизны пространства к нулю). В самой геометрии Лобачевского кривизна отрицательна. Применение его геометрии нашла Бельтрани(траектрисса, псевдосфера), Клейн
Петербургская математическая школа. Остроградский, Буняковский
Хуже всего с математикой было в Москве. В Казани преподавал Лобачевский. Дальше - по хронологии переезжаем в Питер. Там были хорошие математики, но французского воспитания. Основатели Петербуржской математической школы - Остроградский, Буняковский. Профессиональное образование они получали во Франции, где на тот период была самая сильная математика - Коши, Пуассон, Фурье... Буняковский Получал образование в Париже. В 1827 вернулся в Питер, тут же стал академик и адъюнкт. Потом стал вице-президентом Академии Наук. Более 40 работ по теории чисел. Сходимость рядов, свойства, неравенство Буняковского (Буняковского-Шварца, Шварцем было открыто независимо через 16 лет) (интегральное, да), теория чисел. Пятый постулат. Жил 85 лет. Буняковский на дух не переносил теорию Лобачевского. Был первым демографом в России.
Классические проблемы алгебры. Гаусс, Абель, Галуа
Гаусс (1807-1855). Король математиков. В 3-летнем возрасте нашёл у отца ошибку в рассуждениях. Страсть как любил считать. Всё и вся. В 19 лет защитил докторскую диссертацию, в которой доказал основную теорему алгебры, не ссылаясь на то, что корни существуют. Лет через 20 доказал другим способом (более просто). А гордился он решением одночленных уравнений в комплексной плоскости. Построил 17угольник =)
Абель (1802-1829) Занимался уравнениями. Писал работы, отсылал, рецензий нет. Пуассон задвинул Галуа, Абеля - Коши. "Мы не нашли там ни одной разумной мысли". Пытался найти формулу для решения уравнений выше 4й степени. Отрицательный результат - может быть тоже положительным результатом... Доказал, что не существует общих формул для нахождения общих решений выше 4 для произвольных уравнений. Признак сходимости рядов Абеля. Интегрировал сложные функции, теория эллиптических и гиперэллиптических интегралов. Этой проблемой занималась ещё Ковалевская потом, на основе результатов Абеля. Он поправил Коши - в критерии равномерной сходимости. Всегда был беден, занимался частными уроками...
Эварест Галуа. (жил 21 год) В школе набунтовал и был очень умным. Активный борец с королевской властью. Анархист, республиканец... работы - тоже бунтарские. Попытался поступить в Высшую Политехническую Школу. Ему задавали очень сложные вопросы, он показывал пренебрежение к таким простым вопросам, за что его не взяли. Второй раз пошёл поступать. Не способным. Поступил в "нормальную" школу. Её закончил, продолжил писать труды в области алгебры. Поставил перед собой цель решить проблему разрешимости уравнений высоких степеней. Ввёл новые алгебраические образования - группы. Попал в тюрьму за ссору с директором, когда вышел - поссорился с другом (из-за либо политических разногласий, либо из-за девушки). Результат - дуэль, и перед дуэлью написал на всякий случай все свои результаты, их потом долго понимали.)
Становление современного математического анализа. Научная биография О. Коши
Матанализ. Проблема - приведение матана к современному виду.
Коши. Он перестроил весь матан на основе теории пределов (имхо лектора). Опубликовал 789 работ. (у Эйлера было побольше, да..) Области: диффуры, задача Коши, теоремы существования и единственности ДУЧП, ОДУ, работы по геометрии, алгебре, теории чисел, оптика, механика, ТФКП, читал курс лекций в политехническом институте. Начинает с понятия функции, классификация функций, разложение в степенные ряды, ввёл нормальное понятие бесконечно малой величины (через пробел). Непрерывность функции стандартизовал. Признак сходимости Коши. Критерий сходимости Коши для числовой последовательности. Сходимость рядов. Были и неверные теоремы сформулированы. Абель поправил его.)
Научные достижения Б. Больцано и К. Вейерштрасса
Больцано
Он преподавал богословие в Чехии. С точки зрения властей был очень неблагонадёжен. В конце концов его попросили со службы, и он удалился в деревню, где занимался математикой. И именно поэтому он не очень известен. В 1817 году доказал первые серьёзные теоремы. Дал строгое определение непрерывности; односторонней непрерывности; свойства её. В 1830 году Больцано построил пример функции, которая непрерывна, но нигде не дифференцируема - в пику Амперу. Если функция непрерывна, то ряд Фурье не обязан сходиться! Но вот построить такую функцию... пример Фейера, пример Колмогорова.
Вейерштрасс.
Развился как известный математик довольно поздно. Понятие предельной точки, всё, что с этим связано. Стал использовать понятия верхней и нижней граней числовых множеств. Достижение верхних и нижних граней. Он заинтересовался вопросом приближения функций многочленами. Активно использовал эпсилон-дельта-язык.
Научная биография П.Л. Чебышева
Пафнутий Львович Чебышёв (1821-1894) Родился в Калужской губернии, зажиточная семья до поры до времени. Поступил в Московский университет. Сделал работу "вычисление корней уравнения", за что получил серебряную медаль. Затем - по теории вероятностей защитил кандидатскую. Докторскую - по теории чисел. Публикаций у него было 80. Но все были исключительно ёмкие, и каждая - на новом уровне. С него началась настоящая теория вероятностей, приближение функций - до него этим никто не занимался. Механика - гениальные результаты. Теория чисел, теория интегрирования, тервер, теория приближения функций и общая теория полиномов. Задача кройки платьев - как поэкономнее. Подбирал проекции для карт, чтобы погрешности были минимальны. Первым сформулировал закон больших чисел; центральную предельную теорему и дал подходы к решению этой теоремы, используя метод моментов. Восстановил ситуацию с недоверием к теорверу (by Остроградский, в частности), вернул репутацию. Исследовал интегрируемость в элементарных функциях хитрых функций. !У него отношение к этому куда более прагматичное. Ему нужно не только знать, что он есть, а его построить. В отличие от Вейерштрасса.
Приближающие многочлены Чебышева
Прежде всего, поговорим о многочленах Чебышёва, приближающих функцию, непрерывную на [a,b]. Возьмем класс многочленов Pn(x). Рассмотрим максимальное уклонение полинома от функции. Поскольку это величина неотрицательная, то есть нижняя грань (напр. 0), следовательно, есть точная нижняя грань. Имеется в виду нижняя грань максимального уклонения среди всех многочленов n-ной степени. Грань называется наилучшим приближением функции. А сам многочлен, на которм она (грань) достигается, называется многочленом наилучшего приближения функции.
Научная биография А.А Маркова (старшего)
А.А.Марков-старший(1856-1922)
Родился в Рязани, долгое время работал в Петербурге. Внес большой вклад в теорию вероятностей и математический анализ. В честь Маркова названы цепи Маркова и неравенство Маркова. Аппарат марковских цепей был позже обобщен Колмогоровым. Цепи Маркова и скрытые марковские модели широко используются в CS.
Научная биография А.М. Ляпунова
А.М.Ляпунов(1857-1910)
Родился в Ярославле, в 1870 семья переезжает в Нижний Новгород.
В 1876 Ляпунов оканчивает гимназию с золотой медалью и поступает в Санкт-Петербургский университет (сначала на факультет естественных наук, затем переходит на математический)
1885 - магистерская диссертация на тему, предложенную Чебышевым (вращение жидкости и фигуры равновесия, возникающие при этом). С этого момента Ляпунов возглавляет кафедру механики в Харьковском университете, читая лекции по всем ее курсам.
1892 - докторская диссертация (задача устойчивости движения системы с конечным числом степеней свободы)
1902 - избирается в Академию Наук, переезжает в Петербург
1905 - книга о фигурах равновесия.
Ляпунов занимался теорией дифференциальных уравнений, гидромеханикой, теорией вероятностей. Основные результаты - в теории устойчивости и движения мехаической системы с конечным числом параметров.
Научная биография С.В. Ковалевской
Софья Ковалевская(1850-1891)
Родилась в 1850 в семье математика, получила хорошее домашнее образование.
В 1869 поступает в Гейдельбергский университет в Германии, в 1870-1874 учится в Берлине у Вейерштрасса.
С 1884 читает лекции в Стокгольмском университете, начав на немецком, но затем довольно быстро освоив шведский.
1888 - золотая медаль Парижской академии наук за открытие третьего классического случая разрешимости задачи о вращении твердого тела.
1891 - умерла от воспаления легких.
Ковалевская занималась астрономией, функциональным анализом, теорией потенциала, математической физикой. Она известна также и своими литературными произведениями (напр., "Нигилистка")
Основоположники теоретических основ программирования и современных ЭВМ
Философские направления в математике. Интуиционизм
отвержение теоретико-множественного подхода к определению математических понятий. Из логики исчезают законы двойного отрицания и исключенного третьего, поэтому становятся возможными только конструктивные доказательства.
Философские направления в математике. Логицизм
математика рассматривается как часть логики; любая математическая теорема в аксиоматической системе может быть рассмотрена как утверждение о логическом следствии. Это дает возможность доказывать теоремы автоматически.
Направление сформулировано Людвигом Готлобом Фреге. Он же попытался свести к логическим понятиям натуральные числа, но потерпел неудачу. Возникший при этом парадокс был обнаружен Бертраном Расселом.
Философские направления в математике. Формализм
попытки получить основание математики с помощью аксиоматических построений. Направление возникло в начале XX века благодаря Давиду Гильберту. Главный тезис – полнота и непротиворечивость.


