МФСП: Оформление задач
Материал из eSyr's wiki.
(дополнение) |
(некоторые добавления) |
||
| Строка 1: | Строка 1: | ||
Как показала практика, на коллоквиумах (и, вероятно, в какой-то степени на экзамене) придираются к оформлению задач. Здесь будут примеры, которые содержат необходимые формальности. Обращаю внимание, что это не мануал по решению и ботать но нему не стоит, это просто пример оформления. | Как показала практика, на коллоквиумах (и, вероятно, в какой-то степени на экзамене) придираются к оформлению задач. Здесь будут примеры, которые содержат необходимые формальности. Обращаю внимание, что это не мануал по решению и ботать но нему не стоит, это просто пример оформления. | ||
| - | == Задача 1== | + | == Задача 1 (EI)== |
Первая задача: по явному описанию функции построить неявное, т.е. переписать первоую часть и добавить пост и пред-условия. | Первая задача: по явному описанию функции построить неявное, т.е. переписать первоую часть и добавить пост и пред-условия. | ||
| - | |||
| - | '''Важно''': в пост-условиях не должно быть локальных переменных | ||
'''Условие''': | '''Условие''': | ||
| Строка 18: | Строка 16: | ||
===Комментарии=== | ===Комментарии=== | ||
| - | Как любезно заметил [http://twitter.com/kornevgen/status/7015914018 kornevgen], дерево рисовать не обязательно:<blockquote>"@dimanium например,все рисуют в 1й задаче дерево,как будто без него не примут задачку!нам же не нужны обезьянки,нам нужны люди!"</blockquote> | + | *Как любезно заметил [http://twitter.com/kornevgen/status/7015914018 kornevgen], дерево рисовать не обязательно:<blockquote>"@dimanium например,все рисуют в 1й задаче дерево,как будто без него не примут задачку!нам же не нужны обезьянки,нам нужны люди!"</blockquote> |
| + | *'''Важно''': в пост-условиях не должно быть локальных переменных и присваиваний | ||
==Задача 2 (AX)== | ==Задача 2 (AX)== | ||
| - | '''Комментарии''': если в сигнатуре функция определена на множестве ВСЕХ входных данных (потому что там -> а не -~->), то нельзя добавлять предусловие в описание функции -- необходимо это условие запихать в тело функции (т.е. если не удовлетворяет ему, то просто не меняется множество). | + | '''Комментарии''': |
| + | * если в сигнатуре функция определена на множестве ВСЕХ входных данных (потому что там -> а не -~->), то нельзя добавлять предусловие в описание функции -- необходимо это условие запихать в тело функции (т.е. если не удовлетворяет ему, то просто не меняется множество). | ||
| + | |||
| + | ==Задача 3 (RFN)== | ||
| + | ==Задача 4 (INV)== | ||
| + | Тут главное -- просто пишите побольше, от души -- и вам поставят полный балл за задачу. ;) | ||
| - | == Задача 5, метод Флойда== | + | == Задача 5 (FL, метод Флойда)== |
===Условие=== | ===Условие=== | ||
<pre> | <pre> | ||
| Строка 58: | Строка 62: | ||
=== Комментарии === | === Комментарии === | ||
| - | Доказательства тождеств приводить не надо (хотя их рекомендуется сделать для уверенности в правильности). В пункте 2 обязательно должны быть явно выписаны условия корректности и завершимости. | + | * Доказательства тождеств приводить не надо (хотя их рекомендуется сделать для уверенности в правильности). В пункте 2 обязательно должны быть явно выписаны условия корректности и завершимости. |
| + | * Не забывать ставить ВСЕ условия прохождений по веткам. | ||
| + | * Помните, что подставлять изменённые значения, необходимо не только в правой части а везде, где они меняются (к примеру, если путь проходит через 2 условия, то второе к оменту вхождение может иметь уже изменённую переменную). | ||
| + | ==Задача 6 (PVS)== | ||
| + | '''ГЛАВНОЕ'''! Убедитесь, что вы доказываете именно теорему, а не лемму или другое какое нибудь дополнительное условие. | ||
{{Курс МФСП}} | {{Курс МФСП}} | ||
Версия 21:37, 19 февраля 2010
Как показала практика, на коллоквиумах (и, вероятно, в какой-то степени на экзамене) придираются к оформлению задач. Здесь будут примеры, которые содержат необходимые формальности. Обращаю внимание, что это не мануал по решению и ботать но нему не стоит, это просто пример оформления.
Содержание |
Задача 1 (EI)
Первая задача: по явному описанию функции построить неявное, т.е. переписать первоую часть и добавить пост и пред-условия.
Условие:
value
f: Int X Int -> write x,y,z Int X Int X Int
f(a,b) as (c,d,e)
f(a,b) is x:=2;
local variable v: Int := 1 in
for i in <.a..a-1+b.> do
v:=i*(x=x+v;i)*2 // (ЗДЕСЬ v не успевает обновиться, т.е идет с предыдущего цикла, т.е. Для x последней итерацией (где v=a-1+b) нет)
end; (y:=z;a,v:=v+1;x,b+v)
end
Комментарии
- Как любезно заметил kornevgen, дерево рисовать не обязательно:
"@dimanium например,все рисуют в 1й задаче дерево,как будто без него не примут задачку!нам же не нужны обезьянки,нам нужны люди!"
- Важно: в пост-условиях не должно быть локальных переменных и присваиваний
Задача 2 (AX)
Комментарии:
- если в сигнатуре функция определена на множестве ВСЕХ входных данных (потому что там -> а не -~->), то нельзя добавлять предусловие в описание функции -- необходимо это условие запихать в тело функции (т.е. если не удовлетворяет ему, то просто не меняется множество).
Задача 3 (RFN)
Задача 4 (INV)
Тут главное -- просто пишите побольше, от души -- и вам поставят полный балл за задачу. ;)
Задача 5 (FL, метод Флойда)
Условие
START
(y1, y2) = (0, x1)
|
-------------->|
| B
| | F
| y2 >= x2-------
| |T |
| | |
(y1, y2) = (y1+1, y2-x2) HALT: (z1, z2) = (y1, y2)
Предусловие: φ(x1, x2): x1 >= 0 ∧ x2 > 0 Постусловие: ψ(x1, x2, z1, z2): x1 = x2*z1 + z2 ∧ z1 < x2
Решение
1. Инвариант в B: P(x1, x2, y1, y2) is φ(x1, x2) ∧ (x1 = x2*y1 + y2) ∧ (y2 >= 0) // в условии не задан, придумываем сами
Имеем 3 пути:
- S-B
- ∀ x1 ∀ x2 [(x1 >= 0) ∧ (x2 > 0) => φ(x1, x2) ∧ (x1 = x2*0 + x1) ∧ (x1 >= 0)] // здесь нужно сразу подставить начальные значения из START, а не писать ∧ (y1 = 0) ∧ (y2 = x1)
- B-T-B
- ∀ x1 ∀ x2 ∀ y1 ∀ y2 [φ(x1, x2) ∧ (x1 = x2*y1 + y2) ∧ (y2 >= 0) ∧ (y2 >= x2) => φ(x1, x2) ∧ (x1 = x2*(y1+1) + (y2-x2)) ∧ ((y2-x2) >= 0)]
- B-F-H
- ∀ x1 ∀ x2 ∀ y1 ∀ y2 [φ(x1, x2) ∧ (x1 = x2*y1 + y2) ∧ (y2 >= 0) ∧ (y2 < x2) => (x1 = x2*y1 + y2) ∧ (y1 < x2)]
2. Фундированное множество - (Nat, >), точка сечения B. Оценочная функция y2.
Условие корректности: ∀ x1 ∀ x2 ∀ y1 ∀ y2 [φ(x1, x2) ∧ (x1 = x2*y1 + y2) ∧ (y2 >= 0) => y2 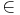 Nat]
Nat]
Условие завершимости: ∀ x1 ∀ x2 ∀ y1 ∀ y2 [φ(x1, x2) ∧ (x1 = x2*y1 + y2) ∧ (y2 >= 0) ∧ (y2 >= x2) => (y2 > y2-x2) ]
Комментарии
- Доказательства тождеств приводить не надо (хотя их рекомендуется сделать для уверенности в правильности). В пункте 2 обязательно должны быть явно выписаны условия корректности и завершимости.
- Не забывать ставить ВСЕ условия прохождений по веткам.
- Помните, что подставлять изменённые значения, необходимо не только в правой части а везде, где они меняются (к примеру, если путь проходит через 2 условия, то второе к оменту вхождение может иметь уже изменённую переменную).
Задача 6 (PVS)
ГЛАВНОЕ! Убедитесь, что вы доказываете именно теорему, а не лемму или другое какое нибудь дополнительное условие.


