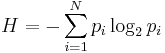ПОД: Ответы старые
Материал из eSyr's wiki.
(→Адресация ОЗУ.) |
(→Расслоение оперативной памяти.) |
||
| Строка 197: | Строка 197: | ||
[[Изображение:Расслоение_ОЗУ.PNG]] | [[Изображение:Расслоение_ОЗУ.PNG]] | ||
| - | При конвейерном доступе при М-кратном расслоении и регулярной выборке | + | При конвейерном доступе при М-кратном расслоении и регулярной выборке на обращение к одной ячейке памяти может тратиться 1/М цикла памяти. Но возможны конфликты по доступу, если шаг регулярной выборки достаточно большой или кратен числу банков памяти. |
= Ассоциативная память. = | = Ассоциативная память. = | ||
Версия 13:10, 20 января 2010
Информация и её измерения.
Термин "информация" происходит от латинского слова "informatio", что означает сведения, разъяснения, изложение. Несмотря на широкое распространение этого термина, понятие информации является одним из самых дискуссионных в науке. В настоящее время наука пытается найти общие свойства и закономерности, присущие многогранному понятию информация, но пока это понятие во многом остается интуитивным и получает различные смысловые наполнения в различных отраслях человеческой деятельности: в обиходе информацией называют любые данные или сведения, которые кого-либо интересуют. Например, сообщение о каких-либо событиях, о чьей-либо деятельности и т.п. "Информировать" в этом смысле означает "сообщить нечто, неизвестное раньше"; в технике под информацией понимают сообщения, передаваемые в форме знаков или сигналов; в кибернетике под информацией понимает ту часть знаний, которая используется для ориентирования, активного действия, управления, т.е. в целях сохранения, совершенствования, развития системы (Н. Винер).
Клод Шеннон, американский учёный, заложивший основы теории информации — науки, изучающей процессы, связанные с передачей, приёмом, преобразованием и хранением информации, — рассматривает информацию как снятую неопределенность наших знаний о чем-то.
Приведем еще несколько определений:
- Информация — это сведения об объектах и явлениях окружающей среды, их параметрах, свойствах и состоянии, которые уменьшают имеющуюся о них степень неопределенности, неполноты знаний (Н.В. Макарова);
- Информация — это отрицание энтропии (Леон Бриллюэн);
- Информация — это мера сложности структур (Моль);
- Информация — это отраженное разнообразие (Урсул);
- Информация — это содержание процесса отражения (Тузов);
- Информация — это вероятность выбора (Яглом).
Современное научное представление об информации очень точно сформулировал Норберт Винер, "отец" кибернетики. А именно: Информация — это обозначение содержания, полученного из внешнего мира в процессе нашего приспособления к нему и приспособления к нему наших чувств.
Подходы к определению количества информации. Формулы Хартли и Шеннона.
Американский инженер Р. Хартли в 1928 г. процесс получения информации рассматривал как выбор одного сообщения из конечного наперёд заданного множества из N равновероятных сообщений, а количество информации I, содержащееся в выбранном сообщении, определял как двоичный логарифм N. Формула Хартли:
Допустим, нужно угадать одно число из набора чисел от единицы до ста. По формуле Хартли можно вычислить, какое количество информации для этого требуется: I = log2100 > 6,644. Таким образом, сообщение о верно угаданном числе содержит количество информации, приблизительно равное 6,644 единицы информации.
Для задач такого рода американский учёный Клод Шеннон предложил в 1948 г. другую формулу определения количества информации, учитывающую возможную неодинаковую вероятность сообщений в наборе. Формула Шеннона:
где pi — вероятность того, что именно i-е сообщение выделено в наборе из N сообщений.
Легко заметить, что если вероятности p1,...,pN равны, то каждая из них равна 1 / N, и формула Шеннона превращается в формулу Хартли.
Помимо двух рассмотренных подходов к определению количества информации, существуют и другие. Важно помнить, что любые теоретические результаты применимы лишь к определённому кругу случаев, очерченному первоначальными допущениями.
В качестве единицы информации Клод Шеннон предложил принять один бит (англ. bit от binary digit — двоичная цифра). Бит в теории информации — количество информации, необходимое для различения двух равновероятных сообщений (типа "орел"—"решка", "чет"—"нечет" и т.п.).
В вычислительной технике битом называют наименьшую "порцию" памяти компьютера, необходимую для хранения одного из двух знаков "0" и "1", используемых для внутримашинного представления данных и команд.
Замечание
"Боюсь соврать, но на одной из первых лекций Фисун задал вопрос как раз на тему а что же такое информация. Ответом, в конечном итоге, явилось, что в современном мире информация - понятие самодостаточное и в пояснениях не нуждаещееся(атомарное, как выразился сам лектор). То есть, по ходу, ответом на вопрос что такое информация будет такое:-"Информация это информация""(c) Источник
Арифметические вычисления до эры ЭВМ.
Первым устройством для счета, известным еще задолго до нашей эры (V в. до н.э.) был простой абак, с которого и началось развитие вычислительной техники. Придумали абак в Греции и Египте.
Греческий (египетский) абак – это дощечка, покрытая слоем пыли, на которой острой палочкой проводились линии и какие-нибудь предметы, размещавшиеся в полученных колонках по позиционному принципу. В Древнем Риме абак появился, вероятно в V–VI вв н.э., и назывался calculi или abakuli. Изготовлялся абак из бронзы, камня, слоновой кости и цветного стекла. До нашего времени дошёл бронзовый римский абак, на котором камешки передвигались в вертикально прорезанных желобках. Внизу помещались камешки для счета до пяти, а в верхней части имелось отделение для камешка, соответствующего пятёрке.
Китайский суан-пан – состояли из деревянной рамки, разделенной на верхние и нижние секции. Палочки соотносятся с колонками, а бусинки с числами. У китайцев в основе счета лежала не десятка, а пятерка. Она разделена на две части: в нижней части на каждом ряду располагаются по 5 косточек, в верхней части – по две. Таким образом, для того чтобы выставить на этих счетах число 6, ставили сначала косточку, соответствующую пятерке, и затем прибавляли одну в разряд единиц.
Японский соробан – прямоугольная рама содержит произвольное количество вертикальных бамбуковых палочек (чем больше их число, тем с большим разрядом цифр можно проводить операции). На каждой палочке по 5 деревянных косточек, разделённых поперечной полосой – над полосой одна косточка, под полосой – 4.
На Руси долгое время считали по косточкам, раскладываемым в кучки. Примерно с XV века получил распространение "дощаный счет", завезенный, видимо, западными купцами вместе с ворванью и текстилем.
«Дощаный счет» – «Русский абак» почти не отличался от обычных счетов и представлял собой рамку с укрепленными горизонтальными веревочками, на которые были нанизаны просверленные сливовые или вишневые косточки. Счеты, которые появились в XV в.в. состоят на особом месте, т.к. используют десятичную, а не пятеричную систему счисления, как все остальные абаки.
Основная заслуга изобретателей абака (какого именно абака? в греко-латинском не было позиционной!) – создание позиционной системы представления чисел. Вычисления на абаке производились перемещением камешке по желобам на доске.
Начало XVII века: вводом понятия логарифма шотландским математиком Джоном Непером и публикацией таблицы логарифмов послужило созданию логарифмической линейки. Одной из первых «вычислительных» машин была суммирующая машина французского ученого Блеза Паскаля, которую изобрел он в 1642 году. Машина Паскаля могла суммировать десятичные числа.
Первую арифметическую машину, выполняющую все четыре арифметических действия, создал в 1673 году немецкий математик Лейбниц – механический арифмометр. Арифметическая машина Лейбница послужила прототипом арифмометров, которые начали производиться серийно с 1820 года и использовались вплоть до 60х годов XX в. Арифмометр был предшественником современного калькулятора. Арифмометр, как и простой калькулятор – это средство механизации вычисления. Человек, производя на таком устройстве, сам управляет его работой, определяет последовательность выполнения операций. XIX в.: автором первого проекта вычислительного автомата был профессор Кембриджского университета английский математик Чарльз Бэббидж.
Аналитическая машина Бэббиджа
Основные идеи заложенные в проекте этой машины, в нашем веке были использованы конструкторами ЭВМ. Все главные компоненты современного компьютера присутствовали в конструкции аналитической машины:
- СКЛАД (в современной технологии – ПАМЯТЬ), где хранятся все исходные числа и промежуточные результаты.
- МЕЛЬНИЦА (арифметическое устройство), в которой осуществляются операции над числами, взятыми из склада.
- КОНТОРА (устройство управления), производящая управление последовательностью операций над числами, соответственно над заданной программой.
- БЛОКИ ВВОДА исходных данных.
- БЛОКИ ПЕЧАТИ РЕЗУЛЬТАТОВ.
Для программного управления использовались перфокарты – картонные карточки с пробитыми в них отверстиями (перфорацией). Проект машины так и не был реализован из-за сложности механического износа деталей проекта, которые опережали технические возможности своего времени, но программы для этой машины были созданы. Их составила дочь Джона Байрона герцогиня Ада Лавлейс, которая по праву считается первым программистом.
Эра электронных вычислительных машин началась в 30-х годах XX в. В 40-х годах удалось создать первую программируемую счетную машину на основе электромеханических реле.
Эволюционная классификация ЭВМ.
Одна из форм классификации ЭВМ - по "поколениям" связана с эволюцией аппаратного и программного оборудования, причем основным классификационным параметром является технология производства. Классификация рассматривается на примерах из отечественной техники, что дает возможность перечислить хотя бы основных творцов отечественной информационной технологии. История отечественных исследований в данной области пока малоизвестна. Это связано с тем, что работы в данной области длительное время носили закрытый характер. В России (в СССР) начало эры вычислительной техники принято вести от 1946г. , когда под руководством Сергея Алексеевича Лебедева закончен проект малой электронной счетной машины (МЭСМ - 50 оп./сек. ОЗУ на 63 команды и 31 константы) - фон Нейманновская универсальная ЭВМ. В 1950/51 гг. она пущена в эксплуатацию. Далее, приводятся некоторые крупные отечественные достижения в области вычислительной техники.
Первое поколение
Первое поколение ЭВМ /1946-1957гг/ использовало в качестве основного элемента электронную лампу. Быстродействие их не превышало 2-3 т. оп./сек; емкость ОЗУ - 2-4 К слов. Это ЭВМ: БЭСМ-1 (В.А. Мельников,1955г.), Минск-1 (И.С. Брук 1952/59 гг.), Урал-4 (Б. И. Рамеев), Стрела (Ю.Я. Базилевский, 1953 г.), М-20 (М.К. Сулим 1860 г. ). А.Н. Мямлиным была разработана и несколько лет успешно эксплуатировалась "самая большая в мире ЭВМ этого поколения" - машина Восток. Программирование для этих машин: однозадачный, пакетный режим, машинный язык, ассемблер (совковый аналог - Автокод).
Второе поколение
В ЭВМ второго поколения /1958-1964гг/ элементной базой служили транзисторы. Отечественные: Урал-14, Минск-22, БЭСМ-4, М-220, Мир-2, Наири и БЭСМ-6 (1 млн. оп./сек , 128К), Весна (В.С. Полин, В.К. Левин), М-10 (М.А. Карцев). ПС-2000, ПС-3000, УМШМ, АСВТ, Сетунь. Программирование: мультипрограммный режим, языки высокого уровня, библиотеки подпрограмм.
Третье поколение
Элементная база ЭВМ третьего поколения, /1965-1971гг/ интегральные схемы - логически законченный функциональный блок, выполненный печатным монтажом. Отечественные ЭВМ этого поколения ЭВМ ЕС (Единой Системы):ЕС-1010,ЕС-1020, ЕС-1066 (2 млн. оп./сек , 8192К) и др. Программирование: мультипрограммный, диалоговый режимы, ОС, виртуальная память.
В 1996 г. в России работают 5 тысяч ЕС ЭВМ из 15 т., уставленных а СССР. НИИЦЭВТ на базе комплектующих IBM/390 разработал 23 модели производительностью от 1.5 до 167 Мфлоп (ЕС1270, ЕС1200, аналоги серверов 9672)). IBM предоставляет также лицензионные программные продукты (ОС-390). Используются в России для сохранения программного задела прикладных систем (проблема наследия ЕС ЭВМ).
Четвертое поколение
ЭВМ четвертого поколения /1972-1977гг/ базируются на "больших интегральных схемах"(БИС) и "микропроцессорах". Отечественные - проект "Эльбрус", ПК. Программирование: диалоговые режимы, сетевая архитектура, экспертные системы.
Пятое поколение
ЭВМ пятого поколения /начиная с 1978г/ используют "сверхбольшие интегральные схемы" (СБИС). Выполненные по такой технологии процессорные элементы на одном кристалле могут быть основным компонентом различных платформ - серверов: от супер-ЭВМ (вычислительных серверов), до интеллектуальных коммутаторов в файл-серверах.
На этом поколении технологические новации приостанавливаются и в восьмидесятые годы в ряде стран появляются проекты создания новых вычислительных систем на новых архитектурных принципах. Так, в 1982 японские разработчики приступили к проекту "компьютерные системы пятого поколения", ориентируясь на принципы искусственного интеллекта, но в 1991 японское министерство труда и промышленности принимает решение о прекращении программы по компьютерам пятого поколения; вместо этого запланировано приступить к разработке компьютеров шестого поколения на основе нейронных сетей.
В СССР под руководством А.Н. Мямлина в рамках такого проекта велась разработка вычислительной системы, состоящей из специализированных процессоров: процессоров ввода/вывода, вычислительного, символьного, архивного процессоров.
В настоящее время в России создаются мультисистемы на базе зарубежных микропроцессоров: вычислительные кластеры (НИИЦЭВТ), супер-ЭВМ МВС-1000 (В.К. Левин, А.В.Забродин). Под руководством Б.А.Бабаяна проектируется микропроцессор Мерсед-архитектектуры. В.С. Бурцев разрабатывает проект суперЭМВ на принципах потоковых машин.
Эволюция отечественного программного обеспечения непосредственно связана с эволюцией архитектуры ЭВМ, первая Программирующая Программа ПП, Интерпретирующая Система- ИС создавались для М-20 (ИПМ). Для ЭВМ этого семейства были реализованы компиляторы с Алгола: ТА-1 (С.С.Лавров), ТФ-2 (М.Р.Шура-Бура), Альфа(А.П.Ершов). Этот абзац нужно написать более понятным языком, если кто-то-таки вкурит, о чём в нём речь
Для БЭСМ-6 создан ряд операционные системы: от Д-68 до ОС ИПМ (Л.Н. Королев, В.П. Иванников, А.Н. Томилин, В.Ф.Тюрин, Н.Н. Говорун, Э.З. Любимский).
Под руководством С.С.Камынина и Э.З. Любимского был реализован проект Алмо: создание машинно-ориентированного языка и на его базе системы мобильных трансляторов.
В.Ф.Турчин предложил функциональный язык Рефал, системы программирования на базе этого языка используются при создании систем символьной обработки и в исследованиях в области метавычислений.
Принципы фон Неймановской архитектуры.
wikipedia:von Neumann architecture
В основу построения подавляющего большинства компьютеров положены следующие общие принципы, сформулированные в 1945 г. американским ученым Джоном фон Нейманом.
Принцип программного управления.
Из него следует, что программа состоит из набора команд, которые выполняются процессором автоматически друг за другом в определенной последовательности. Выборка программы из памяти осуществляется с помощью счетчика команд. Этот регистр процессора последовательно увеличивает хранимый в нем адрес очередной команды на длину команды. А так как команды программы расположены в памяти друг за другом (принцип последовательного программного управления), то тем самым организуется выборка цепочки команд из последовательно расположенных ячеек памяти. Если же нужно после выполнения команды перейти не к следующей, а к какой-то другой, используются команды условного или безусловного переходов, которые заносят в счетчик команд номер ячейки памяти, содержащей следующую команду. (иногда выделяют принцип условного перехода) Выборка команд из памяти прекращается после достижения и выполнения команды “стоп”. Таким образом, процессор исполняет программу автоматически, без вмешательства человека.
Принцип однородности памяти.
Программы и данные хранятся в одной и той же памяти s двоичной системе счисления (иногда выделяют принцип двоичного представления данных). Поэтому компьютер не различает, что хранится в данной ячейке памяти — число, текст или команда. Над командами можно выполнять такие же действия, как и над данными. Это открывает целый ряд возможностей. Например, программа в процессе своего выполнения также может подвергаться переработке, что позволяет задавать в самой программе правила получения некоторых ее частей (так в программе организуется выполнение циклов и подпрограмм). Более того, команды одной программы могут быть получены как результаты исполнения другой программы. На этом принципе основаны методы трансляции — перевода текста программы с языка программирования высокого уровня на язык конкретной машины.
Принцип адресности.
Структурно основная память состоит из перенумерованных ячеек; процессору в произвольный момент времени доступна любая ячейка. Отсюда следует возможность давать имена областям памяти, так, чтобы к запомненным в них значениям можно было впоследствии обращаться или менять их в процессе выполнения программ с использованием присвоенных имен. Компьютеры, построенные на этих принципах, относятся к типу фон-неймановских. Но существуют компьютеры, принципиально отличающиеся от фон-неймановских. Для них, например, может не выполняться принцип программного управления, т.е. они могут работать без “счетчика команд”, указывающего текущую выполняемую команду программы. Для обращения к какой-либо переменной, хранящейся в памяти, этим компьютерам не обязательно давать ей имя. Такие компьютеры называются не-фон-неймановскими.
Виды запоминающих устройств.
Система построена из разнообразных элементов, поэтому для того, чтобы она правильно функционировала, применяются специальные средства, сглаживающие дисбаланс (историческое решение – регистры общего назначения), достигается минимум реальной частоты обращения к памяти - расслоение памяти (это параллельность передачи данных и передача управления). Считывание в память фрагментов данных – организация ассоциативной памяти – кэша (cache) – сверхоперативной памяти, которая аккумулирует наиболее частые команды и минимизирует обращения к оперативной памяти. Также широко используется аппарат прерываний- средство, аппаратно-ориентированное на своевременную обработку поступающей информации, осуществляющее реакцию на ошибки.
Система внешних запоминающих устройств (ВЗУ) компьютера очень широка, она включает в себя типовой набор внешних устройств Традиционно это:
- внешние запоминающие устройства, предназначенные для организации хранения данных и программ;
- устр-ва ввода и отображения, предназначенные для ввода извне данных и программ и отображения этой инф-ции;
- устр-ва приема данных, предназначенные для получения данных от других компьютеров и извне.
Обмен данными:
- записями фиксированного размера – блоками
- записями произвольного размера
Доступ к данным:
- операции чтения и записи (жесткий диск, CDRW).
- только операции чтения (CDROM, DVDROM, …).
По доступу к данным различают устройства:
Последовательного доступа:
В устройствах последовательного доступа для чтения i-ого блока памяти необходимо пройти по первым i-1 блокам. (Пример: пульт дистанционного управления ТВ, кнопки «канал+» и «канал-» или бытовые кассетные магнитофоны - ВЗУ большинства бытовых компьютеров 80-х годов). Устройства последовательного доступа менее эффективны чем устройства прямого доступа.
- Магнитная лента. Это тип ВЗУ широко известный всем пользователям бытовых компьютеров (БК). Его принцип основывается на записи/чтении информации на магнитной ленте. При этом перед началом и после окончания записи на ленту заносится специальный признак - маркер начала или, соответственно, конца. Головка проходит на нужный номер цилиндра и не более чем за 1 оборот находит нужный сектор. Какие блин секторы в магнитной ленте??
Прямого доступа:
В устройствах прямого доступа для того, чтобы прочесть i-ый блок данных, не нужно читать первые i-1 блоков данных. (Пример: пульт дистанционного управления Вашего телевизора, кнопки - каналы; для того, чтобы посмотреть i-ый канал не нужно «перещелкивать» первые i-1).
- Магнитные диски. Конструкция ВЗУ данного типа состоит в том, что имеется несколько дисков (компьютерный жаргон - «блины»), обладающих возможностью с помощью эффекта перемагничивания хранить информацию, размещенных на оси, которые вращаются с некоторой постоянной скоростью. Каждый такой диск имеет одну или две поверхности, покрытые слоем, позволяющим записывать информацию
- Магнитный барабан.металлический цилиндр большой массы, вращающийся вокруг своей оси. Роль большой массы - поддержание стабильной скорости вращения. Поверхность этого цилиндра покрыта магнитным слоем, позволяющим хранить, читать и записывать информацию. Поверхность барабана разделена на n равных частей (в виде колец), которые называются треками (track). Над барабаном расположен блок неподвижных головок так, что над каждым треком расположена одна и только одна головка. (Головок, соответственно, тоже n штук). Головки способны считывать и записывать информацию с барабана. Каждый трек разделен на равные сектора. В каждый момент времени в устройстве может работать только одна головка. Запись информации происходит по трекам барабана, начиная с определенного сектора. При заказе на обмен поступают следующие параметры: № трека, № сектора, объем информации.
- Магнито-электронные ВЗУ прямого доступа (память на магнитных доменах). В конструкции этого устройства опять-таки используется барабан, но на этот раз он неподвижен. Барабан опять-таки разделен на треки и над каждым треком имеется своя головка. За счет некоторых магнитно-электрических эффектов происходит перемещение по треку цепочки доменов. При этом каждый домен однозначно ориентирован, то есть он бежит стороной, с зарядом «+», либо стороной, заряженной «-». Так кодируется ноль и единица. Эта память очень быстродейственна, т.к. в ней нет «механики». Память на магнитных доменах очень дорога и используется в большинстве случаев в военной и космической областях.
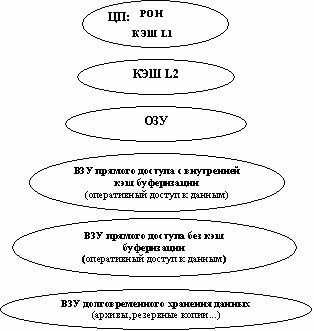
Иерархия памяти
Выглядит следующим образом:
Адресация ОЗУ.
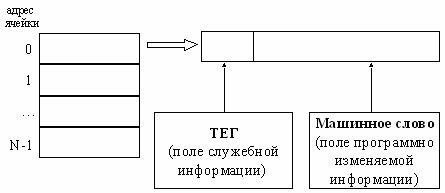
ОЗУ - устройство, предназначенное для хранения оперативной информации. В ОЗУ размещается исполняемая в данный момент программа и используемые ею данные. ОЗУ состоит из ячеек памяти, каждая из которых содержит поле машинного слова и поле служебной информации.
Машинное слово – поле программно изменяемой информации, в машинном слове могут располагаться машинные команды (или части машинных команд) или данные, которыми может оперировать программа. Машинное слово имеет фиксированный для данной ЭВМ размер (обычно размер машинного слова – это количество двоичных разрядов, размещаемых в машинном слове). Служебная информация (иногда ТЭГ) – поле ячейки памяти, в котором схемами контроля процессора и ОЗУ автоматически размещается информация, необходимая для осуществления контроля за целостностью и корректностью использования данных, размещаемых в машинном слове.
Использование содержимого поля служебной информации
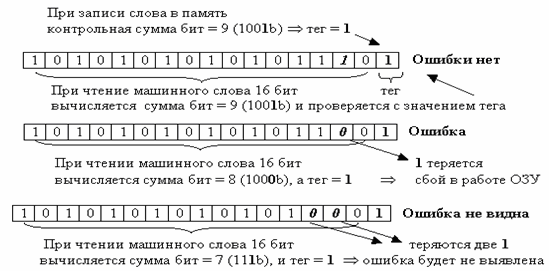
- контроль за целостностью данных.: (при записи машинного слова подсчет числа единиц в коде машинного слова и дополнение до четного или нечетного в контрольном разряде), при чтении контроль соответствия; Пример контроля за целостностью данных по четности:
- контроль доступа к командам/данным (обеспечение блокировки передачи управления на область данных программы или несанкционированной записи в область команд);
- контроль доступа к машинным типам данных – осуществление контроля за соответствием машинной команды и типа ее операндов;
Конкретная структура, а также наличие поля служебной информации зависит от конкретной ЭВМ.
В ОЗУ все ячейки памяти имеют уникальные имена, имя - адрес ячейки памяти. Обычно адрес – это порядковый номер ячейки памяти (нумерация ячеек памяти возможна как подряд идущими номерами, так и номерами, кратными некоторому значению). Доступ к содержимому машинного слова осуществляется посредством использования адреса. Производительность оперативной памяти – скорость доступа процессора к данным, размещенным в ОЗУ.
- время доступа (access time - taccess) – время между запросом на чтение слова из оперативной памяти и получением содержимого этого слова.
- длительность цикла памяти (cycle time – tcycle) – минимальное время между началом текущего и последующего обращения к памяти.
tcycle > taccess: мы можем быстро получить значение из памяти, но ей ещё нужно время восстановиться.
Обычно скорость доступа к данным ОЗУ существенно ниже скорости обработки информации в ЦП. (tcycle >> tprocess). Необходимо, чтобы итоговая скорость выполнения команды процессором как можно меньше зависела от скорости доступа к коду команды и к используемым в ней операндам из памяти. Это составляет проблему, которая системным образом решается на уровне архитектуры ЭВМ.
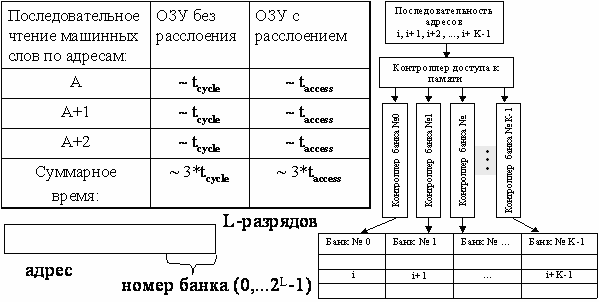
Расслоение оперативной памяти.
Расслоение ОЗУ – один из аппаратных путей решения проблемы дисбаланса в скорости доступа к данным, размещенным в ОЗУ и производительностью ЦП. Суть расслоения ОЗУ состоит в следующем. Все ОЗУ состоит из k блоков, каждый из которых может работать независимо. Ячейки памяти распределены между блоками таким образом, что у любой ячейки ее соседи размещаются в соседних блоках. Возможность предварительной буферизации при чтении команд/данных. Оптимизация при записи в ОЗУ больших объемов данных.
При конвейерном доступе при М-кратном расслоении и регулярной выборке на обращение к одной ячейке памяти может тратиться 1/М цикла памяти. Но возможны конфликты по доступу, если шаг регулярной выборки достаточно большой или кратен числу банков памяти.
Ассоциативная память.
Оперативную память (ОП) можно представить в виде двумерной таблицы, строки которой хранят в двоичном коде команды и данные. Обращения за содержимом строки производится заданием номера (адреса) нужной строки. При записи, кроме адреса строки указывается регистр, содержимое которого следует записать в эту строку. Запись занимает больше времени, чем чтение. Пусть в памяти из трех строк хранятся номера телефонов.
| 1924021 |
| 9448304 |
| 3336167 |
Для получения номера телефона второго абонента следует обратиться: load (2) и получить в регистре ответа R = 9448304. Такой вид памяти, при котором необходимая информация определяется номером строки памяти, называется адресной. Другой вид оперативной памяти – ассоциативной можно рассматривать также как двумерную таблицу, но у каждой строки которой есть дополнительное поле, поле ключа.
Например:
| Ключ | Содержимое |
|---|---|
| Иванов | 1924021 |
| Петров | 9448304 |
| Сидоров | 3336167 |
После обращение к ассоциативной памяти с запросом : load (Петров) для данного примера получим ответ: R = 9448304. Здесь задание координаты строки памяти производится не по адресу, а по ключу. Но при состоянии ассоциативной памяти:
| Ключ | Содержимое |
|---|---|
| 1 | 1924021 |
| 2 | 9448304 |
| 3 | 3336167 |
можно получить номер телефона из второй строки запросом: load (2). Таким образом на ассоциативной памяти можно моделировать работу адресной. Ассоциативная память имеет очевидное преимущества перед адресной, однако, у нее есть большой недостаток - ее аппаратная реализация невозможна для памяти большого объема.
ВОПРОС: Предложите схему реализации модели ассоциативной памяти при помощи адресной.
Ответ: Область памяти делим ровно пополам. Первая половина заполняется ключами, вторая соответствующими ключам значениями. Когда найден ключ, известен его адрес как смещение относительно начала памяти. Тогда адрес содержимого по ключу – это смещение + размер области ключей, то есть адрес ячейки из второй половины памяти, которая соответствует ключу.
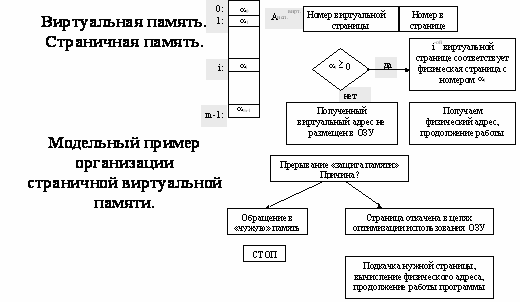
Виртуальная память.
Внутри программы к моменту образования исполняемого модуля используется модель организации адресного пространства программы (эта модель, в общем случае не связана с теми ресурсами ОЗУ, которые предполагается использовать позднее). Для простоты будем считать, что данная модель представляет собой непрерывный фрагмент адресного пространства в пределах которого размещены данные и команды программы. Будем называть подобную организацию адресации в программе программной адресацией или логической/виртуальной адресацией.
Итак, повторяем, на уровне исполняемого кода имеется программа в машинных кодах, использующая адреса данных и команд. Эти адреса в общем случае не являются адресами конкретных физических ячеек памяти, в которых размещены эти данные, более того, в последствии мы увидим, что виртуальным (или программным) адресам могут ставиться в соответствие произвольные физические адреса памяти. То есть при реальном исполнении программы далеко не всегда виртуальная адресация, используемая в программе совпадает с физической адресацией, используемой ЦП при выполнении данной программы.
Базирование адресов.
Элементарное программно-аппаратное решение – использование возможности базирования адресов.
Суть его состоит в следующем: пусть имеется исполняемый программный модуль. Виртуальное адресное пространство этого модуля лежит в диапазоне [0, Aкон]. В ЭВМ выделяется специальный регистр базирования Rбаз., который содержит физический адрес начала области памяти, в которой будет размещен код данного исполняемого модуля. При этом исполняемые адреса, используемые в модуле будут автоматически преобразовываться в адреса физического размещения данных путем их сложения с регистром Rбаз.. Таким образом код используемого модуля может. Эта схема является элементарным решением организации простейшего аппарата виртуальной памяти. Аппарат виртуальной памяти – аппаратные средства компьютера, обеспечивающие преобразование (установление соответствия) программных (виртуальных) адресов, используемых в программе адресам физической памяти в которой размещена программа при выполнении.
Пусть имеется вычислительная система, функционирующая в мультипрограммном режиме. То есть одновременно в системе обрабатываются несколько программ/процессов. Один из них занимает ресурсы ЦП. Другие ждут завершения операций обмена, третьи – готовы к исполнению и ожидают предоставления ресурсов ЦП. При этом происходит завершение выполнявшихся процессов и ввод новых, это приводит к возникновению проблемы фрагментации ОЗУ. Суть ее следующая. При размещении новых программ/процессов в ОЗУ ЭВМ (для их мультипрограммной обработки) образуются свободные фрагменты ОЗУ между программами/процессами. Суммарный объем свободных фрагментов может быть достаточно большим, но, в то же время, размер самого большого свободного фрагмента недостаточно для размещения в нем новой программы/процесса. В этой ситуации возможна деградация системы – в системе имеются незанятые ресурсы ОЗУ, но они не могут быть использованы. Путь решения этой проблемы – использование более развитых механизмов организации ОЗУ и виртуальной памяти, позволяющие отображать виртуальное адресное пространство программы/процесса не в одну непрерывную область физической памяти, а в некоторую совокупность областей.
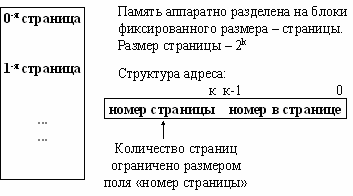
Страничная организация памяти
Страничная организация памяти предполагает разделение всего пространства ОЗУ на блоки одинакового размера – страницы. Обычно размер страницы равен 2k. В этом случае адрес, используемый в данной ЭВМ, будет иметь следующую структуру:
Модельная (упрощенная) схема организации функционирования страничной памяти ЭВМ следующая: Пусть одна система команд ЭВМ позволяет адресовать и использовать m страниц размером 2k каждая. То есть виртуальное адресное пространство программы/процесса может использовать для адресации команд и данных до m страниц.
Физическое адресное пространство – оперативная память, подключенная к данному компьютеру. Физическое адресное пространство, в общем случае может иметь произвольное число физических страниц (их может быть больше m, а может быть и меньше). Соответственно структура исполнительного физического адреса будет отличаться от структуры исполнительного виртуального адреса за счет размера поля ”номер страницы”.
В виртуальном адресе размер поля определяется максимальным числом виртуальных страниц – m.
В физическом адресе – максимально возможным количеством физических страниц, которые могут быть подключены к данной ЭВМ (это также фиксированная аппаратная характеристика ЭВМ).
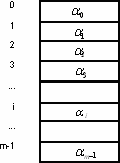
В ЦП ЭВМ имеется аппаратная таблица страниц (иногда таблица приписки) следующей структуры:
Таблица содержит m строк. Содержимое таблицы определяет соответствие виртуальной памяти физической для выполняющейся в данный момент программы/процесса. Соответствие определяется следующим образом: i-я строка таблицы соответствует i-й виртуальной странице. Содержимое строки αi определяет, чему соответствует i-я виртуальная страница программы/процесса. Если αi ≥ 0, то это означает, что αi есть номер физической страницы, которая соответствует виртуальной странице программы/процесса. Если αi= -1, то это означает, что для i-й виртуальной страницы нет соответствия физической странице ОЗУ (обработка этой ситуации ниже).
Итак, рассмотрим последовательность действий при использовании аппарата виртуальной страничной памяти.
- При выполнении очередной команды схемы управления ЦП вычисляют некоторый адрес операнда (операндов) Aисп. Это виртуальный исполнительный адрес.
- Из Aисп. Выделяются значимые поля номер страницы (номер виртуальной страницы). По этому значению происходит индексация и доступ к соответствующей строке таблицы страниц.
- Если значение строки ≥ 0, то происходит замена содержимого поля номер страницы на соответствующее значение строки таблицы, таким образом, получается физический адрес. И далее ЦП осуществляет работу с физическим адресом. Если значение строки таблицы равно –1 это означает, что полученный виртуальный адрес не размещен в ОЗУ. Причины такой ситуации? Их две. Первая – данная виртуальная страница отсутствует в перечне станиц, доступных для программы/процесса, то есть имеет место попытка обращения в “ чужую”, не легитимную память. Вторая ситуация, когда операционная система в целях оптимизации использования ОЗУ, откачала некоторые страницы программы/процесса в ВЗУ(свопинг).
Алгоритмы управления страницами ОЗУ.
Проблема загрузки «новой» страницы в память. Необходимо выбрать страницу для удаления из памяти (с учетом ее модификации и пр.) Существуют разные алгоритмы:
Алгоритм NRU
(Not Recently Used – "не использовавшийся в последнее время"), который спользует биты статуса страницы в записях таблицы страниц. R - обращение, M - изменение. Эти биты устанавливаются аппаратно.
- При запуске процесса M и R для всех страниц процесса обнуляются
- По таймеру происходит обнуление всех битов R
- При возникновении страничного прерывания ОС делит все страниц на классы по изменению.
- Случайная выборка страницы для удаления в непустом классе с минимальным номером
Стратегия: лучше выгрузить измененную страницу, к которой не было обращений как минимум в течение 1 «тика» таймера, чем часто используемую страницу
Алгоритм FIFO
«Первым прибыл – первым удален» - простейший вариант FIFO. (проблемы «справедливости»)
Модификация алгоритма (алгоритм вторая попытка):
- Выбирается самая «старая страница». Если R=0, то она заменяется
- Если R=1, то R – обнуляется, обновляется время загрузки страницы в память (т.е. переносится в конец очереди). На п.1
Алгоритм «Часы»
- Если R=0, то выгрузка страницы и стрелка на позицию вправо.
- Если R=1, то R-обнуляется, стрелка на позицию вправо и на П.1.
Алгоритм LRU
Least Recently Used – наиболее давно используемая страница
Вариант реализации:
- Памяти N страниц. Существует битовая матрица NxN (изначально полностью обнулена).
- При каждом обращении к i-ой странице происходит присваивание 1 всем битам i-ой строки и 0 - всем битам i-ого столбца.
- Строка с наименьшим двоичным кодом - искомая
Алгоритм NFU
Not Frequently Used – редко использовавшаяся страница (Программная модификация LRU (?))
Для каждой физической страницы i – программный счетчик Counti0. Изначально Counti – обнуляется для всех i.
- По таймеру Counti = Counti + Ri (R - бит обращения)
- Выбор страницы с минимальным значением {Counti}
Недостаток – «помнит» всю активность по использованию страниц
Модификация NFU – алгоритм старения
- Значение счетчика сдвигается на 1 разряд вправо.
- Значение R добавляется в крайний левый разряд счетчика.
Использование в ЭВМ принципа локальности вычислений.
Полностью ассоциативная кэш-память.
Кэш-память с прямым отображением.
Частично-асссоциативная кэш-память.
Изменение данных в кэш памяти.
Учет параметров кэша при программировании задач.
Конвейерная обработка данных.
Внеочередное выполнение команд.
Производительность конвейеров.
Векторно-конвейерные вычислители.
Конвейерная обработка команд.
Конвейерные конфликты.
Спекулятивное выполнение команд.
Статическое предсказание условных переходов.
Механизмы динамического предсказания переходов.
Обработка условных операторов в EPIC.
Эволюция системы команд микропроцессоров.
Суперскалярные микропроцессоры.
Широкоформатные команды для параллельной обработки данных.
Проект EPIC.
Мультитредовые, многоядерные вычислители.
Классификация параллельных вычислителей по Флинну.
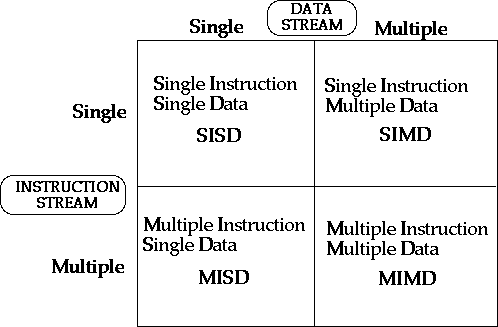
По-видимому, самой ранней и наиболее известной является классификация архитектур вычислительных систем, предложенная в 1966 году М.Флинном. Классификация базируется на понятии потока, под которым понимается последовательность элементов, команд или данных, обрабатываемая процессором. На основе числа потоков команд и потоков данных Флинн выделяет четыре класса архитектур: SISD,MISD,SIMD,MIMD. Эти четыре класса архитектур схематически представляются в виде квадрата, называемого квадратом Флинна.
SISD
SISD (single instruction stream / single data stream) -- одиночный поток команд и одиночный поток данных. К этому классу относятся, прежде всего, классические последовательные машины, или иначе, машины фон-неймановского типа, например, PDP-11 или VAX 11/780. В таких машинах есть только один поток команд, все команды обрабатываются последовательно друг за другом и каждая команда инициирует одну операцию с одним потоком данных. Не имеет значения тот факт, что для увеличения скорости обработки команд и скорости выполнения арифметических операций может применяться конвейерная обработка -- как машина CDC 6600 со скалярными функциональными устройствами, так и CDC 7600 с конвейерными попадают в этот класс.
SIMD
SIMD (single instruction stream / multiple data stream) - одиночный поток команд и множественный поток данных. В архитектурах подобного рода сохраняется один поток команд, включающий, в отличие от предыдущего класса, векторные команды. Это позволяет выполнять одну арифметическую операцию сразу над многими данными - элементами вектора. Способ выполнения векторных операций не оговаривается, поэтому обработка элементов вектора может производится либо процессорной матрицей, как в ILLIAC IV, либо с помощью конвейера, как, например, в машине CRAY-1.
Машины типа SIMD.
Машины типа SIMD состоят из большого числа идентичных процессорных элементов, имеющих собственную память. Все процессорные элементы в такой машине выполняют одну и ту же программу. Очевидно, что такая машина, составленная из большого числа процессоров, может обеспечить очень высокую производительность только на тех задачах, при решении которых все процессоры могут делать одну и ту же работу. Модель вычислений для машины SIMD очень похожа на модель вычислений для векторного процессора: одиночная операция выполняется над большим блоком данных.
В отличие от ограниченного конвейерного функционирования векторного процессора, матричный процессор (синоним для большинства SIMD-машин) может быть значительно более гибким. Обрабатывающие элементы таких процессоров - это универсальные программируемые ЭВМ, так что задача, решаемая параллельно, может быть достаточно сложной и содержать ветвления. Обычное проявление этой вычислительной модели в исходной программе примерно такое же, как и в случае векторных операций: циклы на элементах массива, в которых значения, вырабатываемые на одной итерации цикла, не используются на другой итерации цикла.
Модели вычислений на векторных и матричных ЭВМ настолько схожи, что эти ЭВМ часто обсуждаются как эквивалентные.
MISD
MISD (multiple instruction stream / single data stream) - множественный поток команд и одиночный поток данных. Определение подразумевает наличие в архитектуре многих процессоров, обрабатывающих один и тот же поток данных. Однако ни Флинн, ни другие специалисты в области архитектуры компьютеров до сих пор не смогли представить убедительный пример реально существующей вычислительной системы, построенной на данном принципе. Ряд исследователей [3,4,5] относят конвейерные машины к данному классу, однако это не нашло окончательного признания в научном сообществе. Будем считать, что пока данный класс пуст.
MIMD
MIMD (multiple instruction stream / multiple data stream) - множественный поток команд и множественный поток данных. Этот класс предполагает, что в вычислительной системе есть несколько устройств обработки команд, объединенных в единый комплекс и работающих каждое со своим потоком команд и данных.
Машины типа MIMD.
Термин "мультипроцессор" покрывает большинство машин типа MIMD и (подобно тому, как термин "матричный процессор" применяется к машинам типа SIMD) часто используется в качестве синонима для машин типа MIMD. В мультипроцессорной системе каждый процессорный элемент (ПЭ) выполняет свою программу достаточно независимо от других процессорных элементов. Процессорные элементы, конечно, должны как-то связываться друг с другом, что делает необходимым более подробную классификацию машин типа MIMD. В мультипроцессорах с общей памятью (сильносвязанных мультипроцессорах) имеется память данных и команд, доступная всем ПЭ. С общей памятью ПЭ связываются с помощью общей шины или сети обмена. В противоположность этому варианту в слабосвязанных многопроцессорных системах (машинах с локальной памятью) вся память делится между процессорными элементами и каждый блок памяти доступен только связанному с ним процессору. Сеть обмена связывает процессорные элементы друг с другом.
Базовой моделью вычислений на MIMD-мультипроцессоре является совокупность независимых процессов, эпизодически обращающихся к разделяемым данным. Существует большое количество вариантов этой модели. На одном конце спектра - модель распределенных вычислений, в которой программа делится на довольно большое число параллельных задач, состоящих из множества подпрограмм. На другом конце спектра - модель потоковых вычислений, в которых каждая операция в программе может рассматриваться как отдельный процесс. Такая операция ждет своих входных данных (операндов), которые должны быть переданы ей другими процессами. По их получении операция выполняется, и полученное значение передается тем процессам, которые в нем нуждаются. В потоковых моделях вычислений с большим и средним уровнем гранулярности, процессы содержат большое число операций и выполняются в потоковой манере.
Примеры и особенности
Итак, что же собой представляет каждый класс? В SISD, как уже говорилось, входят однопроцессорные последовательные компьютеры типа VAX 11/780. Однако, многими критиками подмечено, что в этот класс можно включить и векторно-конвейерные машины, если рассматривать вектор как одно неделимое данное для соответствующей команды. В таком случае в этот класс попадут и такие системы, как CRAY-1, CYBER 205, машины семейства FACOM VP и многие другие.
Бесспорными представителями класса SIMD считаются матрицы процессоров: ILLIAC IV, ICL DAP, Goodyear Aerospace MPP, Connection Machine 1 и т.п. В таких системах единое управляющее устройство контролирует множество процессорных элементов. Каждый процессорный элемент получает от устройства управления в каждый фиксированный момент времени одинаковую команду и выполняет ее над своими локальными данными. Для классических процессорных матриц никаких вопросов не возникает, однако в этот же класс можно включить и векторно-конвейерные машины, например, CRAY-1. В этом случае каждый элемент вектора надо рассматривать как отдельный элемент потока данных.
Класс MIMD чрезвычайно широк, поскольку включает в себя всевозможные мультипроцессорные системы: Cm*, C.mmp, CRAY Y-MP, Denelcor HEP,BBN Butterfly, Intel Paragon, CRAY T3D и многие другие. Интересно то, что если конвейерную обработку рассматривать как выполнение множества команд (операций ступеней конвейера) не над одиночным векторным потоком данных, а над множественным скалярным потоком, то все рассмотренные выше векторно-конвейерные компьютеры можно расположить и в данном классе.
Предложенная схема классификации вплоть до настоящего времени является самой применяемой при начальной характеристике того или иного компьютера. Если говорится, что компьютер принадлежит классу SIMD или MIMD, то сразу становится понятным базовый принцип его работы, и в некоторых случаях этого бывает достаточно. Однако видны и явные недостатки. В частности, некоторые заслуживающие внимания архитектуры, например dataflow и векторно--конвейерные машины, четко не вписываются в данную классификацию. Другой недостаток - это чрезмерная заполненность класса MIMD. Необходимо средство, более избирательно систематизирующее архитектуры, которые по Флинну попадают в один класс, но совершенно различны по числу процессоров, природе и топологии связи между ними, по способу организации памяти и, конечно же, по технологии программирования.
Наличие пустого класса (MISD) не стоит считать недостатком схемы. Такие классы, по мнению некоторых исследователей в области классификации архитектур [6,7], могут стать чрезвычайно полезными для разработки принципиально новых концепций в теории и практике построения вычислительных систем.
Статические коммутационные сети.
Динамические коммутаторы.
Метакомпъютинг.
Вычислительные кластеры.
Матричные параллельные мультипроцессоры.
Симметричные мультипроцессоры.
Архитектура памяти cc-NUMA.
cc-NUMA – “неоднородный доступ к памяти с поддержкой когерентности кэшей”. Логически память NUMA системы представляется единым сплошным массивом, но распределена между узлами. Любые изменения сделанные каким-либо процессором в памяти становятся доступны всем процессорам благодаря механизму поддержания когерентности кэшей. Архитектура cc-NUMA предполагает кэширование как вертикальных (процессор - локальная память) так и горизонтальных (узел - узел) связей. Кэширование вертикальных связей позволяет организовать каждый узел как UMA компьютер, позволяя получить преимущества UMA архитектуры используя небольшое количество процессоров (обычно 2 или 4) над общей памятью и увеличивая тем самым производительность до 4 раз. В тоже время, возможность комбинирования в одной вычислительной системе множества узлов UMA данной архитектуры позволяет наращивать мощность, не увеличивая слишком количества процессоров в каждом узле. А это позволяет использовать преимущества UMA архитектур, и одновременно имея большое количество процессоров в одной вычислительной системе.
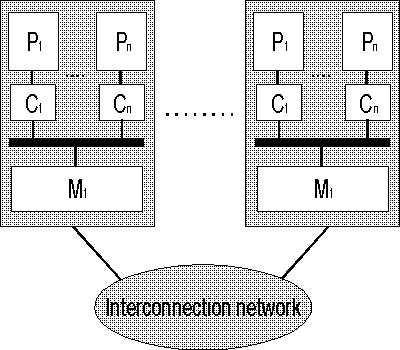
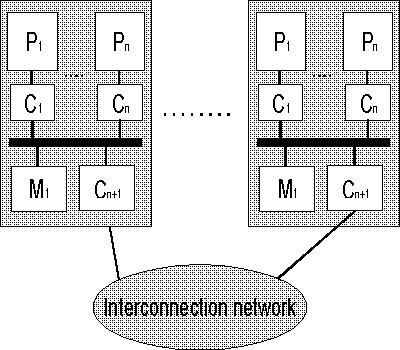
На рисунке ниже представлены различия между NUMA и cc-NUMA архитектурами:
Общая структура архитектуры NUMA
Общая структура архитектуры cc-NUMA.
Обозначения: P – процессор, С – кэш, М – память, Interconnection network – соединяющая сеть.
В системе CC-NUMA физически распределенная память объединяется, как в любой другой SMP-архитектуре, в единый массив. Не происходит никакого копирования страниц или данных между ячейками памяти. Адресное пространство в данных архитектурах делится между узлами. Данные, хранящиеся в адресном пространстве некоторого узла, физически хранятся в этом же узле. Нет никакой программно - реализованной передачи сообщений. Существует просто одна карта памяти, с частями, физически связанными медным кабелем, и очень умные (в большей степени, чем объединительная плата) аппаратные средства. Аппаратно - реализованная кэш-когерентность означает, что не требуется какого-либо программного обеспечения для сохранения множества копий обновленных данных или для передачи их между множеством экземпляров ОС и приложений. Со всем этим справляется аппаратный уровень точно так же, как в любом SMP-узле, с одной копией ОС и несколькими процессорами.
Парадигмы программирования для параллельных вычислителей.
Нетрадиционные вычислители.
Организация вычислений на графе.
Реализация потоковых машин.
Нейронные сети как вычислители.
Измерения производительности ЭВМ.
Реальная и полная производительность вычислителей.
Пакеты для измерения производительности вычислительных систем.
Параметры рейтинга ТОР500.
Закон Амдала.
Закон Амдала показывает коэффициент ускорения выполнения программы на параллельных системах в зависимости от степени распараллеливания программы. Пусть: N - число процессоров системы, P - доля распараллеливаемой части программы, а S = 1-P - доля скалярных операций программы, выполняемых без совмещения по времени.( S+P = 1 , S,P >= 0). Тогда, по Амдалу, общее время выполнения программы на однопроцессорном вычислителе S+P, на мультипроцессоре: S+P/N, а ускорение при этом есть функция от P: Sp = (S+P)/(S+P/N) = 1/(S+P/N).
Из формулы закона Амдала следует,что при:
P = 0 S = 1 - ускорения вычисления нет, а
P = 1 S = 0 - ускорение вычислений в N раз
Если P = S = 0.5, то даже при бесконечном числе процессоров ускорение не может быть более чем в 2 раза.
Параллельные алгоритмы. Метрики.
Параллельные алгоритмы редукции.
Распараллеливание алгоритмов рекурсии первого порядка.
При рекурсивных операциях значение каждого очередного члена последовательности или элемента структуры зависит от значений одного или нескольких предшествующих членов. На ИГ (информационном графе) рекурсия отражается последовательностью одинаковых подграфов, так что результаты предшествующего подграфа являются исходными данными для последующего. В последовательных ЭВМ рекурсия реализуется в виде циклических процессов. Рекурсия встречается не только при числовой обработке, но и при обработке сигналов, операциями над символами и т.п. Рекурсивный характер обработки накладывает ограничения на возможности распараллеливания, которое может быть достигнуто лишь реорганизацией последовательности обработки.
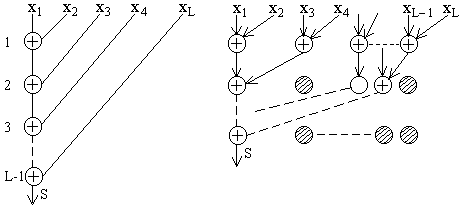
Остановимся на простейшем примере линейной рекурсии первого порядка для вычисления суммы S = xi всех элементов вектора X = xi,i = 1,2,...,L; для нахождения этой суммы можно воспользоваться рекурсивным соотношением S: = Si − 1 + xi,i = 1,2,...,L.
Информационный граф на Рис.1а иллюстрирует рекурсивный способ вычисления суммы, и поскольку каждый из операндов используется однократно, такой граф представляет собой бинарное дерево. Если выполнение каждой примитивной операции занимает интервал t, то суммарные затраты времени (и длина графа q) при реализации этого ИГ составят t = (L − 1) * t;q = (L − 1).
При наличии нескольких вычислителей очевидно, что такой алгоритм будет неэффективным, и задача состоит в том, чтобы минимизировать высоту дерева. Преобразование выполняется в соответствии с законами коммутативности, ассоциативности и дистрибутивности, в результате чего может быть получен трансформированный ИГ, показанный на Рис.1б.
Высота такого дерева q' = [log2 > L], а длительность реализации составит t' = t[log2 > L] в предположении, что операции реализуются за то же время t и что затраты времени на обмен между отдельными вычислителями эквивалентны затратам времени на обмен между ячейкой памяти и вычислителем в последовательной структуре. Такой метод нахождения суммы элементов вектора получил название метода сдваивания или метода нахождения параллельных каскадных сумм.
Максимальное ускорение t / t' можно оценить как O(L / log L);оно достигается при числе вычислителей не менее N = L / 2, причем полностью все L / 2 вычислители загружены только на первом шаге вычислений, на последнем шаге используется лишь один вычислитель.
Не используемые на каждом шаге вычислители можно отразить на ИГ в виде "пустых" операторов, которые показаны на Рис.1б в виде заштрихованных кружочков. Эти пустые операторы не имеют входных и выходных дуг. Теперь можно оценить эффективность полученного алгоритма как отношение числа действительных к общему действительных и пустых операторов. Очевидно, что понятие эффективности сродни понятию коэффициента полезного действия.
Для рассматриваемого алгоритма эффективность составляет 1/2 и не зависит от L.
Векторизация последовательных программ.
Синхронизация параллельных процессов.
Исполняемые комментарии в языках программирования.
Система Open MP.
OpenMP (Open Multi-Processing) это набор директив компилятора, библиотечных процедур и переменных окружения, которые предназначены для программирования многопоточных приложений на многопроцессорных системах с единой памятью на языках C, C++ и Fortran.
Разработку спецификации OpenMP ведут несколько крупных производителей вычислительной техники и программного обеспечения, чья работа регулируется некоммерческой организацией, называемой OpenMP Architecture Review Board (ARB).
OpenMP реализует параллельные вычисления с помощью многопоточности, в которой «главный» (master) поток создает набор подчиненных (slave) потоков и задача распределяется между ними. Предполагается, что потоки выполняются параллельно на машине с несколькими процессорами (количество процессоров не обязательно должно быть больше или равно количеству потоков).
Задачи, выполняемые потоками параллельно, также как и данные, требуемые для выполнения этих задач, описываются с помощью специальных директив препроцессора соответствующего языка — прагм. Например, участок кода на языке Fortran, который должен исполняться несколькими потоками, каждый из которых имеет свою копию переменной N, предваряется следующей директивой: !$OMP PARALLEL PRIVATE(N)
Количество создаваемых потоков может регулироваться как самой программой при помощи вызова библиотечных процедур, так и извне, при помощи переменных окружения.
Ключевыми элементами OpenMP являются
* конструкции для создания потоков (директива parallel), * конструкции распределения работы между потоками (директивы DO/for и section), * конструкции для управления работой с данными (выражения shared и private), * конструкции для синхронизации потоков (директивы critical, atomic и barrier), * процедуры библиотеки поддержки времени выполнения (например, omp_get_thread_num), * переменные окружения (например, OMP_NUM_THREADS).
Ниже приведены примеры программ с использованием директив OpenMP: Fortran 77
В этой программе на языке Fortran создается заранее неизвестное число потоков (оно определяется переменной окружения OMP_NUM_THREADS перед запуском программы), каждый из которых выводит приветствие вместе со своим номером. Главный поток (имеющий номер 0) также выводит общее число потоков, но только после того, как все они «пройдут» директиву BARRIER.
PROGRAM HELLO
INTEGER ID, NTHRDS
INTEGER OMP_GET_THREAD_NUM, OMP_GET_NUM_THREADS
C$OMP PARALLEL PRIVATE(ID)
ID = OMP_GET_THREAD_NUM()
PRINT *, 'HELLO WORLD FROM THREAD', ID
C$OMP BARRIER
IF ( ID .EQ. 0 ) THEN
NTHRDS = OMP_GET_NUM_THREADS()
PRINT *, 'THERE ARE', NTHRDS, 'THREADS'
END IF
C$OMP END PARALLEL
END
В этой программе на языке С два вектора (a и b) складываются параллельно десятью потоками.
#include <stdio.h>
#include <omp.h>
#define N 100
int main(int argc, char *argv[])
{
float a[N], b[N], c[N];
int i;
omp_set_dynamic(0); // запретить библиотеке openmp менять число потоков во время исполнения
omp_set_num_threads(10); // установить число потоков в 10
// инициализируем векторы
for (i = 0; i < N; i++)
{
a[i] = i * 1.0;
b[i] = i * 2.0;
}
// вычисляем сумму векторов
#pragma omp parallel shared(a, b, c) private(i)
{
#pragma omp for
for (i = 0; i < N; i++)
c[i] = a[i] + b[i];
}
printf ("%f\n", c[10]);
return 0;
}
OpenMP поддерживается многими коммерческими компиляторами.
- Компиляторы Sun Studio поддерживают официальную спецификацию — OpenMP 2.5 [2] - с улучшенной производительностью под ОС Solaris; поддержка Linux запланирована на следующий релиз.
- Visual C++ 2005 поддерживает OpenMP в редакциях Professional и Team System [3].
- GCC 4.2 поддерживает OpenMP, а некоторые дистрибутивы (такие как Fedora Core 5 gcc) включили поддержку в свои версии GCC 4.1.
- Intel C Compiler
- IBM XL compiler
- PGI (Portland group)
- Pathscale
- HP
Пакет MPI.
Язык Фортран-GNS.
Порождение параллельных процессов. Идентификация абонентов.
Протоколы передачи сообщений.
Учет топологии кластера в МР программировании.
Язык Фортран-DVM.
DVM-система предоставляет единый комплекс средств для разработки параллельных программ научно-технических расчетов на языках Си и Фортран 77.
Модель параллелизма DVM. Модель параллелизма DVM базируется на модели параллелизма по данным. Аббревиатура DVM отражает два названия модели: распределенная виртуальная память (Distributed Virtual Memory) и распределенная виртуальная машина (Distributed Virtual Mashine). Эти два названия указывают на адаптацию модели DVM как для систем с общей памятью, так и для систем с распределенной памятью. Высокоуровневая модель DVM позволяет не только снизить трудоемкость разработки параллельных программ, но и определяет единую формализованную базу для систем поддержки выполнения, отладки, оценки и прогноза производительности.
Языки и компиляторы. В отличие от стандарта HPF в системе DVM не ставилась задача полной автоматизации распараллеливания вычислений и синхронизации работы с общими данными. С помощью высокоуровневых спецификаций программист полностью управляет эффективностью выполнения параллельной программы. С другой стороны, при проектировании и развитии языка Fortran DVM отслеживалась совместимость с подмножеством стандартов HPF1 и HPF2.
Единая модель параллелизма встроена в языки Си и Фортран 77 на базе конструкций, которые “невидимы” для стандартных компиляторов, что позволяет иметь один экземпляр программы для последовательного и параллельного выполнения. Компиляторы с языков C-DVM и Fortran DVM переводят DVM-программу в программу на соответствующем языке (Си или Фортран 77) с вызовами функций системы поддержки параллельного выполнения. Поэтому единственным требованием к параллельной системе является наличие компиляторов с языков Си и Фортран 77.
Технология выполнения и отладки. Единая модель параллелизма позволяет иметь для двух языков единую систему поддержки выполнения и, как следствие, единую систему отладки, анализа и прогноза производительности. Выполнение и отладка DVM-программ может осуществляться в следующих режимах: Последовательное выполнение и отладка средствами стандартных компиляторов с языков Си и Фортран 77. Псевдо-параллельное выполнение на рабочей станции (среда WINDOWS и UNIX). Параллельное выполнение на параллельной ЭВМ.
При псевдо-параллельном и параллельном выполнении возможны следующие режимы отладки: автоматическая проверка правильности директив параллелизма; трассировка и сравнение результатов параллельного и последовательного выполнения; накопление и визуализация трассировки данных; накопление данных о производительности и прогноз производительности параллельного выполнения.
Язык Fortran DVM (FDVM) представляет собой язык Фортран 77 [5], расширенный спецификациями параллелизма. Эти спецификации оформлены в виде специальных комментариев, которые называются директивами. Директивы FDVM можно условно разделить на три подмножества:
- Распределение данных
- Распределение вычислений
- Спецификация удаленных данных
Модель параллелизма FDVM базируется на специальной форме параллелизма по данным: одна программа – множество потоков данных (ОПМД). В этой модели одна и та же программа выполняется на каждом процессоре, но каждый процессор выполняет свое подмножество операторов в соответствии с распределением данных.
В модели FDVM пользователь вначале определяет многомерный массив виртуальных процессоров, на секции которого будут распределяться данные и вычисления. При этом секция может варьироваться от полного массива процессоров до отдельного процессора.
На следующем этапе определяются массивы, которые должны быть распределены между процессорами (распределенные данные). Эти массивы специфицируются директивами отображения данных. Остальные переменные (распределяемые по умолчанию) отображаются по одному экземпляру на каждый процессор (размноженные данные). Размноженная переменная должна иметь одно и то же значение на каждом процессоре за исключением переменных в параллельных конструкциях.
Модель FDVM определяет два уровня параллелизма: параллелизм по данным на секции массива процессоров; параллелизм задач – независимые вычисления на секциях массива процессоров.
Параллелизм по данным реализуется распределением витков тесно-гнездового цикла между процессорами. При этом каждый виток такого параллельного цикла полностью выполняется на одном процессоре. Операторы вне параллельного цикла выполняются по правилу собственных вычислений.
Параллелизм задач реализуется распределением данных и независимых вычислений на секции массива процессоров.
При вычислении значения собственной переменной процессору могут потребоваться как значения собственных переменных, так и значения несобственных (удаленных) переменных. Все удаленные переменные должны быть указаны в директивах доступа к удаленным данным.
Система программирования НОРМА.
Язык Норма является специализированным языком и предназначен для спецификации численных методов решения задач математической физики. Изначально он был ориентирован на решение задач математической физики разностными методами, однако, как показала практика, может быть использован для решения более широкого класса вычислительных задач.
Первоначально термин Норма расшифровывался следующим образом: Непроцедурное Описание Разностных Моделей Алгоритмов. Сейчас мы считаем уместной и другую трактовку - это Нормальный уровень общения прикладного математика с ЭВМ: расчетные формулы, полученные им в процессе решения прикладной задачи, почти непосредственно используются для ввода в вычислительную систему и проведения счета.
В записи на Норме не требуется никакой информации о порядке счета, способах организации вычислительных (циклических) процессов. Порядок предложений языка может быть произвольным -- информационные взаимосвязи выявляются и учитываются транслятором при организации вычислительного процесса. Программа на языке Норма может рассматриваться как описание запроса на вычисление, а реализация этого запроса с учетом архитектуры ЭВМ и возможностей выходного языка - то есть синтез выходной программы - возлагается на транслятор.
Выбор уровня языка Норма определяет характерную его черту - это язык с однократным присваиванием, то есть каждая переменная может принимать значение только один раз. Такие понятия, как память, побочный эффект, оператор присваивания, управляющие операторы в языке Норма отсутствуют по определению.
Эти свойства, и некоторые другие ограничения (в первую очередь, на вид индексных выражений и способы описания индексных пространств), позволяют строго обосновать разрешимость задачи синтеза выходной программы [2,3], так как в достаточно общей постановке решение этой задачи приводит к значительным математическим трудностям - она может оказаться NP-полной либо вообще неразрешимой. С другой стороны, исследования, связанные с разработкой и применением языка Норма показывают, что имеющиеся ограничения приемлемы с практической точки зрения [5].
Программа на Норме состоит из одного или нескольких разделов. Разделы могут быть трех видов - главный раздел, простой раздел и раздел-функция, вид раздела определяется ключевыми словами MAIN PART, PART, FUNCTION соответственно.
Разделы могут вызывать друг друга по имени и передавать данные при помощи механизма формальных и фактических параметров, или через внешние файлы при помощи описаний INPUT и OUTPUT. Для каждого раздела справедливо правило локализации: имена, описанные в разделе, локализованы в этом разделе; понятие глобальных переменных в языке отсутствует.
Главный раздел обязательно должен присутствовать в программе на Норме и быть единственным; формальных параметров он не имеет. Вызовы главного раздела, а также рекурсивные вызовы разделов запрещены. В заголовке раздела указывается имя раздела и список формальных параметров. Формальные параметры должны быть описаны в теле раздела при помощи declaration-of-scalar-variables, declaration-of-variables-on-domains или declaration-of-external
Параметры-величины, указанные до ключевого слова RESULT в списке формальных параметров, являются исходными данными для вычислений, описываемых в разделе; параметры, перечисленные после - являются результатами вычислений. Один и тот же параметр не может быть одновременно исходным и результатом: это приводит к переприсваиванию значений переменным (повторному присваиванию), что запрещено в Норме. В разделе-функции ключевое слово RESULT не используется: результат вычисления функции связывается с именем и типом функции.
В теле раздела могут быть заданы описания, операторы и итерации (порядок их расположения, вообще говоря, произвольный - возможные ограничения определяются при описании входного языка транслятора).
Система Норма состоит из следующих компонентов:
- Декларативный язык Норма
- Компилятор с языка Норма
- Конфигуратор программ на языке Норма
- Отладчик программ на языке Норма
- Пользовательский Windows-интерфейс
Особенности машинной арифметики.
Погрешности параллельных вычислений. Оценить ошибки суммирования.
Источники погрешности при вычислениях на параллельных системах. В общем случае, арифметические операции над элементами дискретного подмножества вещественных чисел F не корректны. Результат арифметических операций чисел с плавающей запятой может: - иметь абсолютное значение, больше M (максимального числа) - машинное переполнение; - иметь ненулевое значение, меньшее m (минимального числа) по абсолютной величине - машинный нуль; - иметь значение в диапазоне [m:M] и тем не не менее не принадлежать множеству F (произведение двух чисел из F, как правило, записывается посредством 2t либо 2t-1 значащих цифр); Поэтому, на множестве чисел с плавающей запятой определяются и "плавающие" арифметические операции, за результаты которых, если они не выходит за границы множества F, принимается ближайшие по значению элементы F. Примеры из четырехразрядной десятичной арифметики по Н. Вирту. А) Пусть x=9.900 y=1.000 z=-0.999 и тогда: 1 (x+y)+z = 9.910 2 x+(y+z) = 9.901 В) Пусть x=1100. y=-5.000 z=5.001 и тогда: 1 (x*y)+(x*z) = 1.000 2 x*(y+z) = 1.100 Здесь операции + и * - плавающие машинные операции. Такие 'чиcленные' процессы называют иногда 'неточными', здесь нарушаются ассоциативный и дистрибутивный законы арифметики..
Оценить полную ошибку для суммирования положительных чисел.
Пример расчета полной ошибки для суммирования положительных чисел
Формула полной ошибки для суммирования положительных чисел Ai (i=1,..,n) имеет вид: 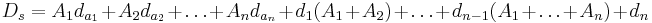 , где
, где
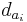 - относительные ошибки представления чисел в ЭВМ, а di - относительные ошибки округления чисел при каждой следующей операции сложения. Пусть: все
- относительные ошибки представления чисел в ЭВМ, а di - относительные ошибки округления чисел при каждой следующей операции сложения. Пусть: все 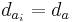 и di = d, a
и di = d, a 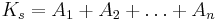 , тогда:
, тогда: ![D_s = d_aK_s + d[(n-1)A_1+(n-1)A_2 + (n-2)A_3 + \dots+ 2A_{n-1} + A_n]](/w/images/math/2/c/9/2c9a96b06bc14bb7f38a85a37bda2f09.png) Очевидно, что наибольший "вклад" в сумму ошибок вносят числа, суммируемые вначале. Следовательно, если суммируемые положительные числа упорядочить по возрастанию, максимально возможная ошибка суммы будет минимальной. Изменяя порядок суммирования чисел можно получать различные результаты. Но если даже слагаемые отличаются друг от друга незначительно, на точность результата может оказать влияние способ суммирования.
Очевидно, что наибольший "вклад" в сумму ошибок вносят числа, суммируемые вначале. Следовательно, если суммируемые положительные числа упорядочить по возрастанию, максимально возможная ошибка суммы будет минимальной. Изменяя порядок суммирования чисел можно получать различные результаты. Но если даже слагаемые отличаются друг от друга незначительно, на точность результата может оказать влияние способ суммирования.
Пусть суммируются 15 положительных чисел, тогда ошибка результата: 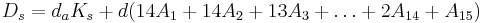 .
Слагаемое daKs не зависит от способа суммирования, и далее не учитывается. Пусть слагаемые имеют вид: Ai = A0 + ei, где
.
Слагаемое daKs не зависит от способа суммирования, и далее не учитывается. Пусть слагаемые имеют вид: Ai = A0 + ei, где 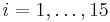 , тогда:
, тогда: 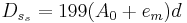 , где
, где 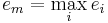 , d - ошибка округления при выполнении арифметической операции сложения.
Если провести суммирование этих чисел по группам (три группы по четыре числа и одна группа из трех чисел), то ошибки частных сумм имеют вид:
, d - ошибка округления при выполнении арифметической операции сложения.
Если провести суммирование этих чисел по группам (три группы по четыре числа и одна группа из трех чисел), то ошибки частных сумм имеют вид:
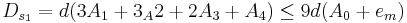
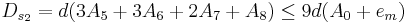
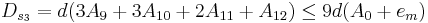
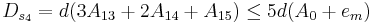
Полная оценка ошибок округления будет 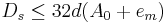 , что меньше
, что меньше
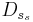 . Итак суммирование по группам дает меньшую ошибку результата.
Например, разделив процесс суммирования массива положительных чисел на параллельные процессы, и затем получив сумму частных сумм, можно получить результат, отличный от последовательного суммирования в одном процесс.
. Итак суммирование по группам дает меньшую ошибку результата.
Например, разделив процесс суммирования массива положительных чисел на параллельные процессы, и затем получив сумму частных сумм, можно получить результат, отличный от последовательного суммирования в одном процесс.
Алгоритмы оптимизации программ, влияющие на точность вычислений.
Оптимизационные преобразования программ для их оптимального выполнения на конвейерных вычислителях могут проводиться системами программирования. Эти преобразования, алгебраически эквивалентные, могут нарушить порядок вычислений, предписанный исходным текстом программы. Последствия таких преобразований обсуждались выше. Наиболее характерные преобразования следующие.
1. Балансировка дерева вычислений
Балансировка дерева вычислений (tree-height reduction or balancing) выражений позволяют использовать конвейерное АУ без пропуска рабочих тактов. Так, вычисление суммы вещественных чисел: A+B+C+D+E+F+G+H, будет запрограммировано как последовательность операций: (((A+B)+(C+D))+((E+F)+(G+H))); это нарушает заданную по умолчанию последовательность вычислений с накоплением одной частной суммы и может повлиять на результат.
2. Исключение общих подвыражений
Алгоритмы исключения общих подвыражений (Common subexpession elimination) также могут изменить порядок вычислений. Если компилятор распознает в выражениях повторяющееся вычисление, то это вычисление производятся один раз, его результат сохраняется на регистре, и в дальнейшем используется этот регистр. Тем самым исключается избыточность вычислений.
X = A + B + C + D ----> REG = B + C
Y = B + E + C X = A + D + REG
Y = E + REG
3. Разворачивание циклов
Разворачивание циклов (loop unrolling) - расписывание цикла последовательностью операторов присваивания: либо полностью, либо размножение тела цикла с некоторым коэффициентом (фактором) размножения. Производится частичное или полное разворачивание цикла в последовательный участок кода. При частичном разворачивании используется так называемый фактор разворачивания (который можно задавать в директиве компилятору).
DO I=1,100 DO I=1,100,4
A(I) = B(I) + C(I) A(I) = B(I) + C(I)
ENDDO A(I+1) = B(I+1) + C(I+1)
A(I+2) = B(I+2) + C(I+2)
A(I+3) = B(I+3) + C(I+3)
ENDDO
При этом преобразовании снижается количество анализов итерационной переменной. Данный алгоритм также может привести к нарушению предписанного первоначально порядка вычислений. Например:
DO I=1,10 DO I=1,10,2
S = S + A(I) S = S + A(I)
ENDDO S1 = S1 + A(A+1)
ENDDO
S = S + S1
Здесь, суммирование проводится отдельно для четных и нечетных элементов с последующем сложением частных сумм.