ОКФиКВ, 01 лекция (от 13 февраля)
Материал из eSyr's wiki.
Курс квантовой механики
Введение в квантовую механику, специфическое, такого курса мы не найдём. Это квантовая механика под углом зрения теории информации. Это очень простая КМ, она позволит выроботать квантовую интуицию, позволит понять принцип действия квантового компьютера.
КМ --- наука о микрообъектах --- .... и элементарных частицах.
Начала развиваться в начале прошлого века, в формулы Планка, которая определяет критерии, надо ли описывать объект классически или квантовым образом. Давайте этот критерий введём сразу. Зачем студенты ВМК изучать КМ? Ответ на этот вопрос лектор даст чуть позже. Этот ответ утвердительный, он покажет, что КМ нужно изучить студенту ВМК.
Поскольку у нас есть объект изучеия, микрообъект, то нужны криетрий, которые позволяют его отличить. Пусть у нас есть микрообъект. Этот микрообъект локализован в пространстве Δх и имеет импульс p = mv. Определим произведение p × Δx --- действие. Как мы видим, размерность этой величины --- Дж × с. И в 1908(?) году была Планком введена величина 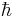 (h с чертой), постоянная Планка, которая равна 10-27 эрг × с. Если действие сравнимо с постоянной Планка
(h с чертой), постоянная Планка, которая равна 10-27 эрг × с. Если действие сравнимо с постоянной Планка 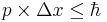 , то этот объект --- микрообъект, и его надо описывать законами микромира.
, то этот объект --- микрообъект, и его надо описывать законами микромира.
Давайте возьмём пример: электрон вразается вокруг ядра, величина его локализации --- 10-8 см, скорость его порядка 108 см × с, масса порядка 10-27 г, и если перемножим p × Δx ~ 10-27 --- порядка 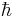 .
.
Рассмотрим другой пример: v ~ 1, m ~ 1, Δx ~ 1, действие --- порядка 1 эрг/с
Между объекта макро- и микромира существует колоссальная разница, и эта разница есть постонная Планка.
КМ --- очень простая наука, матаппарат КМ очень прост. Тем не менее, сами создатели КМ говорят, что КМ никто не понимает. Фейман говорил, что не понимает, Бор говрил, что КМ не понимает тот, кто не испытывает шока. Основная трудность --- в интерпретации матаппаратаа. Матаппарат создан в 1920 годах и существует 100 лет, не только подтверждая, но и предсказывая явления, и одно из щупалец КМ протянулось в область информатики с возможным апофеозом в виде создания КК. Матаппарат работает, созданы технологии, работают, но с интерпретацией проблемы постоянные, постоянные попытки дать интерпретацию отличную от Гейзендбергской интерпретации, мы с ней столкнёмся, она дает реалистическую, необъективную теорию мира. Такие альтернативы существуют, теории скрытых параметров, многих миров, мы могли видеть толстую книжку Дойча, который создал один из первыйх эффективных алогоритмов КК, он также был философм, и он описывал теорию многих миров.
Как сказал лектор, будем рассматривать КМ в приложении к ТИ, которая была создана всего несколько десятков лет назад. И сейчас будет нарисована схема:
История
- 1900 --- зарождение
- 1920---1930 --- развитие
- 1940. изобртение полупроводникового транзистора. Это классичяеский прибор, работающий по законам КМ. Не было бы квантового мира, не было бы его. Транзистор --- классический бит. Начиная с 1950-х годов и по настоящее время полупров. транзистор используется в качестве бита, только размер уменьшается.
- 1960. Лазер. Играет выдающуюся роль в передаче информации: световоды, фотоны как кубиты.
- 2000 (можно 5 лет отять). Квантовая информация
- ? год. Полномасштабный КК. Компьютер, регистор которого основан на квантовых битах, кубитах. Что это такое и как его описывать, познакомимся в курсе.
Прозрачка: По у справа --- число атомов, которым реализуется число бит, по х --- календарное время.
Этот закон показывает, что в районе 2020---2030 года мы получим транзистор, реализуемый 1 атомом. Конечно, когда входишь в новую область, в область КМ, то неизвестно дальнейшее поведение этой прямой. Тем не менее, мир движется к реализации транзистора одним атомом, а атом работает по законам КМ, то это будет кубит, и законы у него совершенно другие.
Для того, чтобы понять, как работаю квантовые приборы, регистры, как решаются простейшие задачи, оценить сложность более реалистических задач (задачи быстрой факторизации), чтобы всё это понимать, необходимо выработать квант. интуицию и понимать это.
Зачем студенту ВМК понимать КМ? Формально мы изучаем физику и это завершающий курс. И всё же каждый культурный человек, тем паче студент ВМК должен знать не в объёме, соотв. научпоп литературе, а глубже, понимать, что творится в этом мире.
Итак, мы закончили введение, теперь приступим к самому курсу, тем не менее, не можем сразу приступить к КМ, необх. ретроспективно клас. физику, частицы и волны -- этот пункт необх. ретроспективно обозреть.
Теоретически изучение сводится к введению модели, и далее изучается матмодель. И если мы проанализируем, какие модели в классич. физике, то обнаружим, что есть всего лишь две модели: модель частици и модель волны. В этих терминах объясняется весь классический мир. Из частиц собираются тела, тела могут быть заряжены, при движ испускаются волны, и так далее. Между част. и полями пост. взаимод, и этим взаим. объячсняется окр. мир.
Почему так? Начнём с того, что такое частица? Частица --- сущность, задаваемая r(t), то есть она локализована. В противоположность, волна делокализована (например, волна на воде). Простейшее описание волны (прост. волновое поле): ψ(x, t) = A sin(ωt - kx) --- простейшая монохроматическая, плоская волна. Почему плоская --- все частицы в опр. плоскостях имеют одну фазу. k --- волновое число, связано с длиной волны λ, k = 2π/λ. В КМ k играет самостоятельную определённую роль. В КМ возникает задача, в самом начале 20-го века, когда эксперимент продвинулся в область микромира, экспериментаторами в разных областях были получены результаты, которые не моглы быть описаны классич. физикой. И они не оставили попытки. Первым описал это Планк. Эксперимент заставил физиков сменить, как говорят философ, парадигму --- набор постулатов в отношении микрочастиц. Вместо того, чтобы рассматривать их как частицы, их начали рассматривать как волны. Это звучит странно, но тем не менее эксперимент заставили экспериментаторов сделать это.
Прозрачка: вверху это картина дифракции рентг. лучей на кристале (в соли). Р. изл. имеет длину волны порядка расст. между атомами. Волны рассеиваются и накладываются. Это т. н. лаограмма(?), которая могла восст. структуру кристалла и многое другое. Этот факт стал известен со времён Рентгена. Что внизу --- картина та же самая по сути, но тут падает то же самое. Один вид картинки заставляет нас сказать, что электрон должен носить волновые свойства.
Ещё прозрачка: это поликристалл (много маленьких кристаллов, повёрнутых под разными углами случ. образом: переход од кристалла к аморфным телам через них, в а. т. они очень маленькие). Картины соверш идентичные от рент. лучей и электронов.
Лектор предупреждает, что мы вынужд. работать без перерыва.
Перейдём к след. очень важному пункту: начинаем под давлением эксперимента строить КМ, а КМ строилась введением постулатом. Если посмотреть на любую науку, то она начинается с постулатов, и всё просто и понятно, пока не дойдём до постулатов и не зададимся вопроса, откуда это. Мы вводим постулаты, которые позвоялют объяснить экспериментальные данные и далее начинаем вводить матаппарат.
Следующий пункт --- дифракция (рассеивание) электронов. Есть какая-то неоднородность в кристалле. Падает излучение, каждый атом рассеивает (лучи дифрагируют на решётке), и потом интерф. картину анализируют. Так вот. Дифракция частиц на кристаллах изучалась впервые Дэвиссоном и Джерменом --- два молодых американца, которые сделали такой эксп.: направили пучок электронов на кристалл никеля. Принципиальная схема: это очень простой эксперимент.
Катод --- кусок металла который нагревается, на который подаётся напряжение, ставится экран, дальше ставится анод --- металл. пластина, на неё поадётся полож. напр, и разность потенциалов равна U. Тогда мы получаем монохром. пучсок электронов. Все эл. имеют одну и ту же энергию, потому что тепловая эн. очень мала, и из закона сохр. eU = mv^2/2 получаем, что все эл. вылетают со скоростью v = sqrt(2eU/m), p = mv = sqrt(2meU), такая простая схема позв. привести электроны в одно сост. В КМ пропадает понятие скорости, она заменяется импульсом.
Этим занимались Д-Ж, и что они получили: ту картину, которую показывали.
Добавим себе немного математики, посмотрим, как эта картина получается: рассм. самую простую модель: есть непр. экран, падает непр. волна, два отверстия в экране (дифракция на двух щелях) --- очень простая матмодель.
От первого отверстия бежит волна под углом Θ e^-i(ωt - kx), вторая волна e^-i(ωt - k(x + δ)), и эти вде волны образуют поле ψ = ψ_1 + ψ_2. Если взять фотпластинку, то получим |ψ^2| --- энергию. В результате получим |ψ_1 + ψ_2|^2 = |A|^2 × |e^ikx + e^ik(x + δ)|^2, 4|A|^2cos^2(kdsin Θ/2), δ = dsinΘ
Аналогично в решётке:
Эти эксперименты были известны до Д-Ж, и были давно проведены в оптике.
Много позже, в наше вемя, повторили этот эксперимент на щелях, меняя пучок электронов. Далее, можно менять напряжение, и тогда будет меняться угол, и Д-Ж это проверили. Но чтобы это проверить, нужно иметь волну, в оптике она известна, а какую использовать для электронов? Они использовали волну де Бройля, он высказал гипотезу, что с каждым электроном связана волна (плоская в простейш случае) ψ = A e^i(kx - ωt), p = hk (h - Планка), hω = p^2/2m, и тогда Д-Ж могли подставить эту формулу, и тогда меняя напряжение, можно подсказать положение максимума и экспериментально подтвердить гипотезу.
Что самое главно, подтверждались не только числа, он и зависимости, и тогда у физиков ничего не оставалосьЮ кроме как принять две гипотезы:
- электорн --- волна
- если электрон имеет импульс p, то он задаётся волной де Бройля.
Планк первым ввёл константу, дальше шло развитие КМ вголубь и вширь, и каждая новая зависимость содержала эту константу.
КМ вводилась под давлением экспериментов, которые делались молодыми учёными, зачастую невежественными. Гейзенберг когда вводил матричную КМ, не знал, что такое матрица.
Тогда встаёт вопрос: какой физический смысл этой волны? Достаточно долгое время ответ на этот вопрос отсутствовал, наконец, Бор дал ответ, опять же, под давлением эксперимента, приходим к этой статичстической интерпретации.
А что, елси один электрон пустим? Это был умозрительный эксперимент до недавнего времени. Пустили один электрон, дифракция на двух щелях (прозрачка). Казалось бы, что будет слабая интерференция. На самом деле см. профр. Получаем вероятностную интерпретацию. Ничего не остаётся, как принять следующее: квадрат модуля волн. функции --- вероятность нахождения электрона в данной точке.
dP(y) = dN(y)dy/N
Тогда коэф. пропорциональности есть плотность вероятности dN(y)/N
Если записать Ψ(r, t), то |Ψ(r, t)|^2 --- вероятность того, что электрон будет находится в t в r
Первый постулат квантовой механики. Любой микрообъект полностью характеризуется заданием функции Ψ(r, t).
Дополнение: волновая функция имеет статистический смысл. Плотность вероятности того, что объект будет обноружен в заданное время в заданном месте.
Что осталось за кадром: почему точка, если есть поле дифракции, то есть это уже поле, а почему точка-то получается? Здесь мы сталкиваемся с основной проблемй превращения функции, котрая содержит фантастическую информацию, при измерении в точку --- коллапс информационного поля волновой функции --- основная проблема алгоритмов КК. Эта информация создаёт несравненный с классическим объём информации, но при измерении получаем всего один бит (по ср. с кубитом). При квантовых выч. получим ту же картину.
Основы квантовой физики и квантовых вычислений
01 02 03 04 05 06 07 08 09 10 11 12
Календарь
Февраль
| 13 | 20 | 27 | ||
Март
| 05 | 12 | 19 | 26 | |
Апрель
| 02 | 09 | 16 | 23 | 30 |


